In my last blog post on plotting functionality in Wolfram|Alpha, we looked at 2D and 3D Cartesian plotting. In this post, we will look at 2D polar and parametric plotting.

For those of you unfamiliar with polar plots, a point on a plane in polar coordinates is located by determining an angle θ and a radius r. For example, the Cartesian point (x, y) = (1, 1) has the polar coordinates (r, θ) = (√2,π/4). The following diagram illustrates the relationship between Cartesian and polar plots.

To generate a polar plot, we need to specify a function that, given an angle θ, returns a radius r that is a function r(θ). Making a polar plot in Wolfram|Alpha is very easy; for example, we can plot Archimedes’ spiral. More »

Wolfram|Alpha is still young and constantly improving. One of the biggest hurdles that our developers are constantly faced with is how to correctly interpret the meaning of general user inputs like “How do I factor an equation?”

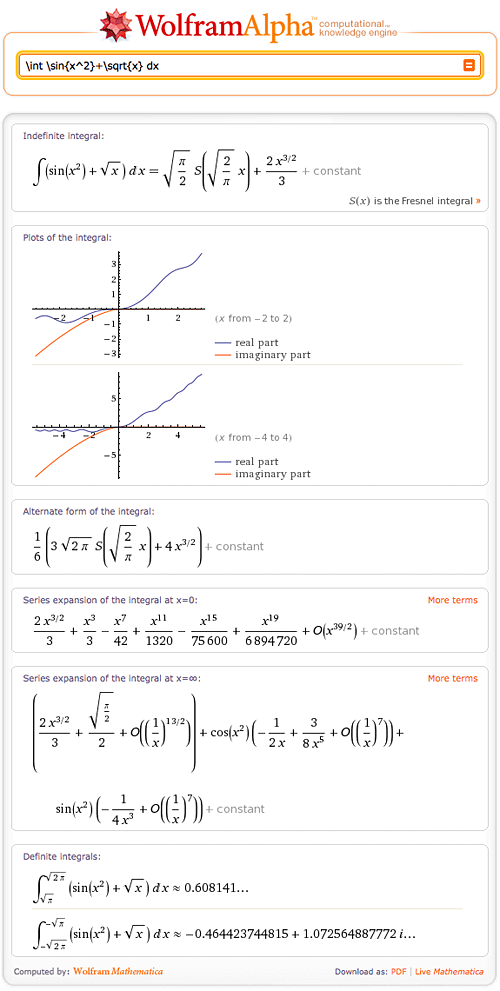
Wolfram|Alpha is great at calculating answers that have specific inputs, but when general concepts are given (like “factoring”, for example), it becomes a bit tricky. How would one calculate a concept like that? Let us look at a specific example—Wolfram|Alpha can easily calculate integrals, as long as you ask it to integrate an explicit function. But what happens when you simply ask Wolfram|Alpha to “integrate”? Before, had you given this input, a number of examples using the word “integrate” would have been generated to show how to properly ask Wolfram|Alpha to calculate an integral. But now, when you enter a generic term or question related to a specific math function or formula, it provides a simple query-specific calculator.

For example, given the query “Show me how to integrate”, the following results appear:

Notice that new input fields appear (as well as optional ones in case the integral is to be calculated within a range, and/or with multiple variables). Similarly, notice how the input fields differ depending on the query: More »

In 1977, famed computer scientist Donald Knuth decided he didn’t like the typesetting of the second edition of The Art of Computer Programming. Rather than unhappily accept the results of photographic typesetting techniques, Knuth invented his own digital typesetting solution, TeX, which would eventually become the standard typesetting system for mathematical and academic content. Wikipedia displays math content using a variant of TeX, and research papers from a large range of fields are very commonly submitted in TeX format.

Our team recently added the ability to understand TeX notation and convert it to the Mathematica form used by the powerful Wolfram|Alpha engine. We’ve received many requests for this functionality from people who use Wolfram|Alpha for advanced math and physics. It’s often easy and natural to write mathematics using TeX, whereas it can otherwise be quite difficult to express clearly in plaintext notation.

The beauty of this new capability is that one can now see, compute, and understand typeset mathematics all through the union of TeX notation and Wolfram|Alpha computation. Complicated expressions are now easily represented using the elegance of TeX: More »

Wolfram|Alpha computes things. While the use of computations to predict the outcomes of scientific experiments, natural processes, and mathematical operations is by no means new (it has become a ubiquitous tool over the last few hundred years), the ease of use and accessibility of a large, powerful, and ever-expanding collection of such computations provided by Wolfram|Alpha is.

Virtually all known processes occur in such a way that certain functionals that describe them become extremal. Typically this happens with the action for time dependent processes and quantities such as the free energy for static configurations. The equations describing the extremality condition of a functional are frequently low-order ordinary and/or partial differential equations and their solutions. For example, for a pendulum: Frechet derivative of Integrate[x'[t]^2/2 – Cos[x[t]], {t, -inf, inf}] wrt x[tau]. Unfortunately, if one uses a sufficiently realistic physical model that incorporates all potentially relevant variables (including things like friction, temperature dependence, deformation, and so forth), the resulting equations typically become complicated—so much so that in most cases, no exact closed-form solution can be found, meaning the equations must be solved using numerical techniques. A simple example is provided by free fall from large heights:

On the other hand, some systems, such as the force of a simple spring, can be described by formulas involving simple low-order polynomial or rational relations between the relevant problem variables (in this case, Hooke’s law, F = k x):

Over the last 200+ years, mathematicians and physicists have found a large, fascinating, and insightful world of phenomena that can be described exactly using these so-called special functions (also commonly known as “the special functions of mathematical physics”), the class of functions that describe phenomena between being difficult and complicated. It includes a few hundred members, and can be viewed as an extension of the so-called elementary functions such as exp(z), log(z), the trigonometric functions, their inverses, and related functions.

Special functions turn up in diverse areas ranging from the spherical pendulum in mechanics to inequivalent representations in quantum field theory, and most of them are solutions of first- or second-order ordinary differential equations. Textbooks often contain simple formulas that correspond to a simplified version of a general physical system—sometimes even without explicitly stating the implicit simplifying assumptions! However, it is often possible to give a more precise and correct result in terms of special functions. For instance, many physics textbooks offer a simple formula for the inductance of a circular coil with a small radius:

While Wolfram|Alpha knows (and allows you to compute with) this simple formula, it also knows the correct general result. In fact, if you just ask Wolfram|Alpha for inductance circular coil, you will be simultaneously presented with two calculators: the one you know from your electromagnetics textbook (small-radius approximation) and the fully correct one. And not only can you compute the results both ways (and see that the results do differ slightly for the chosen parameters, but that the difference can get arbitrarily large), you can also click on the second “Show formula” link (near the bottom of the page on the right side) to see the exact result—which, as can be seen, contains two sorts of special functions, denoted E(m) and K(m) and known as elliptic integrals: More »

Need a tutor for solving equations? Solving equations is just one of hundreds of mathematical tasks that can be done using Wolfram|Alpha. Wolfram|Alpha can solve equations from middle school level all the way through college level and beyond. So next time you are stumped on an equation, consult Wolfram|Alpha for a little help.

Let’s start with the simpler stuff. Wolfram|Alpha can easily solve linear and quadratic equations, and even allows you to view a step-by-step solution of each problem.

What if the roots of the equation are complex? No worries; Wolfram|Alpha has no trouble solving equations over the complex plane.

Wolfram|Alpha can also solve cubic and quartic equations in terms of radicals.

Of course, some solutions are too large or cannot be represented in terms of radicals; Wolfram|Alpha will then return numerical solutions with a “More digits” button. More »

Prior to releasing Wolfram|Alpha into the world this past May, we launched the Wolfram|Alpha Blog. Since our welcome message on April 28, we’ve made 133 additional posts covering Wolfram|Alpha news, team member introductions, and “how-to’s” in a wide variety of areas, including finance, nutrition, chemistry, astronomy, math, travel, and even solving crossword puzzles.

As 2009 draws to a close we thought we’d reach into the archives to share with you some of this year’s most popular blog posts.

April

Rack ’n’ Roll

Take a peek at our system administration team hard at work on one of the
many pre-launch projects. Continue reading…

May

The Secret Behind the Computational Engine in Wolfram|Alpha

Although it’s tempting to think of Wolfram|Alpha as a place to look up facts, that’s only part of the story. The thing that truly sets Wolfram|Alpha apart is that it is able to do sophisticated computations for you, both pure computations involving numbers or formulas you enter, and computations applied automatically to data called up from its repositories.

Why does computation matter? Because computation is what turns generic information into specific answers. Continue reading…

Live, from Champaign!

Wolfram|Alpha just went live for the very first time, running all clusters.

This first run at testing Wolfram|Alpha in the real world is off to an auspicious start, although not surprisingly, we’re still working on some kinks, especially around logging.

While we’re still in the early stages of this long-term project, it is really gratifying to finally have the opportunity to invite you to participate in this project with us. Continue reading…

June

Wolfram|Alpha Q&A Webcast

Stephen Wolfram shared the latest news and updates about Wolfram|Alpha and answered several users’ questions in a live webcast yesterday.

If you missed it, you can watch the recording here. Continue reading… More »

We’re really catching the holiday spirit here at Wolfram|Alpha.

We recently announced our special holiday sale for the Wolfram|Alpha app. Now we are launching our first-ever Wolfram|Alpha “Holiday Tweet-a-Day” contest.

Here’s how it works.

From tomorrow, Tuesday, December 22, through Saturday, January 2, we’ll use Twitter to give away a gift a day. Be the first to retweet our “Holiday Tweet-a-Day” tweet and you get the prize! You can double your chances to win by following and playing along with Wolfram Research.

Start following us today so you don’t miss your chance to win with our Wolfram|Alpha “Holiday Tweet-a-Day” contest.

When we launched Wolfram|Alpha in May 2009, it already contained trillions of pieces of information—the result of nearly five years of sustained data-gathering, on top of more than two decades of formula and algorithm development in Mathematica. Since then, we’ve successfully released a new build of Wolfram|Alpha’s codebase each week, incorporating not only hundreds of minor behind-the-scenes enhancements and bug fixes, but also a steady stream of major new features and datasets.

We’ve highlighted some of these new additions in this blog, but many more have entered the system with little fanfare. As we near the end of 2009, we wanted to look back at seven months of new Wolfram|Alpha features and functionality.

More »

July 17, 2019 Update: Step-by-step solutions has been updated! Learn more.

Have you ever given up working on a math problem because you couldn’t figure out the next step? Wolfram|Alpha can guide you step by step through the process of solving many mathematical problems, from solving a simple quadratic equation to taking the integral of a complex function.

When trying to find the roots of 3x²+x–7=4x, Wolfram|Alpha can break down the steps for you if you click the “Show steps” button in the Result pod.

As you can see, Wolfram|Alpha can find the roots of quadratic equations. Wolfram|Alpha shows how to solve this equation by completing the square and then solving for x. Of course, there are other ways to solve this problem! More »

He’s developing some of the most popular frameworks in Wolfram|Alpha. She’s on the front lines of handling and managing all of your feedback. Meet them both in Part 3 of our video series, “A Moment with the Wolfram|Alpha Developers”:

Other interviews with Wolfram|Alpha team members can be found in Part 1 and Part 2 of this video series.

We’ve updated another entry thanks to feedback sent to Wolfram|Alpha. We’ve now changed linguistic priority settings so that “blog” is no longer interpreted as the math expression b log(x) by default.

More »

Our teams are working hard to meet our goal of having Wolfram|Alpha ready for you in just a few weeks.

Since Stephen Wolfram’s initial announcement, we’ve had the opportunity to show Wolfram|Alpha to some of the thousands of you who contacted us. Many interesting questions surfaced. We plan to use this blog to address those questions and the many more we expect you’ll have as you think about how you too can use Wolfram|Alpha.

We’ll also let you know about upcoming events around Wolfram|Alpha—like the first public preview that Stephen is giving this afternoon at Harvard Law School. Information on participating in the webcast and Q&A can be found here.

Finally, we’ll use this space to talk about ourselves, giving you a peek into our world, what we’re working on, what we’re thinking, and what you can expect from us as the stewards of this project.

So what is Wolfram|Alpha? To begin, we’ve named it a computational knowledge engine.
More »