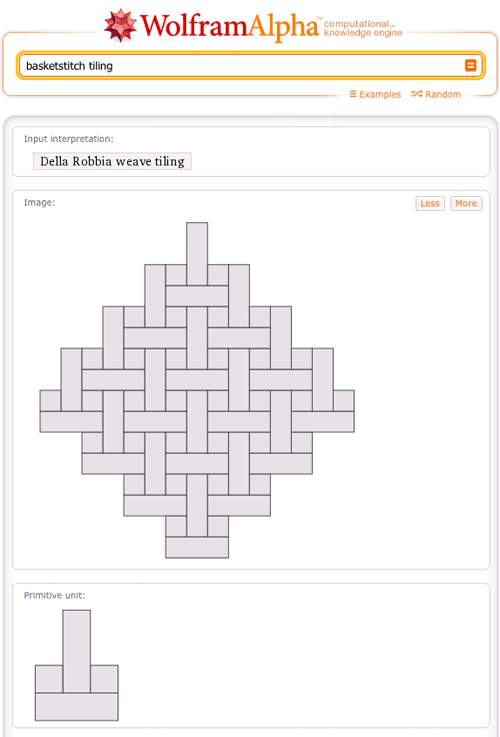
Periodic tilings (also known as tessellations) are often beautiful arrangements of one or more shapes, known as tiles, into regular patterns, which if extended infinitely are capable of covering the entire plane without gaps. Wolfram|Alpha has possessed detailed knowledge on more than 50 common (and uncommon) varieties of periodic tilings for some time, as illustrated, for example, in the case of the basketstitch tiling:

Periodic tilings possess an individual motif (more formally known as a primitive unit) that is repeated iteratively in a predictable (periodic) way. Such tilings are therefore intimately related to the set of symmetry groups of the plane, known as wallpaper groups. While the most general set of geometric similarity (i.e., shape-preserving) operations in the plane includes rotation (change in angle), dilation/expansion (change in size), reflection (flipping about an axis), and translation (change in position), only translation is needed to produce a periodic tiling from a correctly constructed primitive unit. More »