12
12
Things with Wolfram|Alpha are going well. Really well. So well that I’m now incredibly keen to scale them up dramatically.
When I started the Wolfram|Alpha project, I was not even sure anything like it would be possible. But over the last two years we’ve proved that, yes, with the tower of technology we’ve created, one can in fact take large swaths of knowledge, make them computable, and deliver them for everyone to use.
From the outside, it’s easy to see that there’s been steady growth in the domains of knowledge that Wolfram|Alpha covers. And over the next few months there’ll be some big additions, notably in everyday and consumer areas. But to me what’s most dramatic is what’s happened on the inside. Because what we’ve done is to build a giant system of technology and management processes that allows us systematically to make any area of knowledge computable.
The catch is that it always takes effort. We rely on a huge tower of automation. But in every new area we tackle there are new issues, new opportunities—and new ways that resources and human effort have to be used.
I’m very pleased with how broad and deep the coverage we have already achieved is. But we have an immense to-do list, assembled not least from all the feedback we’ve received from users of Wolfram|Alpha. And the good news is that at this point it’s a straight shot: given enough effort, we can complete the to-do list. We have all the systems we need to scale the knowledge in Wolfram|Alpha up all the way. More »
One fall evening in 1843, a man walked past the Brougham Bridge along the Royal Canal in Dublin, Ireland. Suddenly, he felt a flash of insight so strong he was compelled to etch his thoughts into the rock on the side of the bridge. This is what he wrote:
i2 = j2 = k2 = i j k = -1
The man was mathematician William Rowan Hamilton, and the insight was of a number system that could represent forces and motions in three-dimensional space. Hamilton called his numbers “quaternions”, because each has four parts: a real number part, and three other parts labeled with i, j, and k, each of which is also a real number. For example, 2 + 3i + 0.342j – 2k is a quaternion. More »
 2
2

Is it really possible that yet another summer is drawing to a close? Here at Wolfram|Alpha, we’ve spent our summer getting ready to head back to school—building new course assistant apps, adding new data, and even making Wolfram|Alpha interactive with CDF. As the world’s leading knowledge engine, we’ve made it our mission to continually improve and ensure that we’re helping students and teachers around the globe explore concepts, ideas, and calculations on a deeper level than previously possible. More »
 18
18
Back in June we released the Wolfram Physics I Course Assistant to aid those taking introductory physics classes. We are now releasing the Wolfram Physics II Course Assistant for iOS to help those continuing their physics education.
 4
4
The precursors of what we’re trying to do with computable data in Wolfram|Alpha in many ways stretch back to the very dawn of human history—and in fact their development has been fascinatingly tied to the whole progress of civilization.
Last year we invited the leaders of today’s great data repositories to our Wolfram Data Summit—and as a conversation piece we assembled a timeline of the historical development of systematic data and computable knowledge.
This year, as we approach the Wolfram Data Summit 2011, we’ve taken the comments and suggestions we got, and we’re making available a five-feet-long (1.5 meters) printed poster of the timeline—as well as having the basic content on the web.

The story the timeline tells is a fascinating one: of how, in a multitude of steps, our civilization has systematized more and more areas of knowledge—collected the data associated with them, and gradually made them amenable to automation. More »
 10
10
Two weeks ago we made a major announcement: building on technology that we’ve been developing for more than 20 years, we released Computable Document Format (CDF). I think CDF is going to have a big effect on the way all sorts of things can be communicated. Because for the first time it makes it practical to include live computation as a routine part of a document.
There are many important applications of CDF that we’ll no doubt be seeing over the months and years to come. But today I’m pleased to announce an experimental one from us: Wolfram|Alpha with CDF.
Starting today, as soon as you have the free CDF plugin installed (or if you have Mathematica 8 on your system) you can go to the top right-hand corner of the Wolfram|Alpha website, and set CDF on, with the result that Wolfram|Alpha will generate not just a static web page, but instead full CDF output—that you can directly interact and compute with. More »
Recently we released our pregnancy data content, accessible through various queries such as “pregnant 18 weeks” or “pregnant, fetus’s weight 5 lbs 4 oz”. To add to that data, we have created an Apgar score calculator and assessment tool.
The Apgar score is a value assigned to newborn babies within the first 5 to 10 minutes of life. This value is a quick assessment of the baby’s overall health based on 5 variables: the color of the baby’s body and extremities, pulse, reaction (e.g., facial expression, cry response) to stimulation of the nose or feet, muscle tension after stimulation, and respiratory activity. All of these variables can be described more simply as appearance, pulse, grimace, activity, and respiration. Not so coincidentally, the first letters of these descriptions form an acronym that corresponds to the physician who developed the scale, Dr. Virginia Apgar. More »
 16
16
Today we are releasing our Wolfram Pre-Algebra Course Assistant App for iOS, expanding our planned series of Course Assistant Apps built using Wolfram|Alpha technology.
 2
2
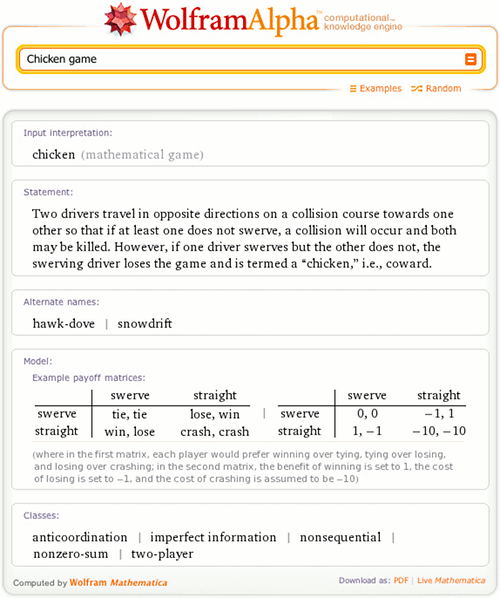
Game theory is a rich branch of mathematics that deals with the analysis of games, where, mathematically speaking, a “game” can be defined as a conflict involving gains and losses between two or more opponents who follow formal rules.
Mathematical games can be very simple, such as the game of chicken (which is not recommended in practice):
 9
9
Planning a trip can be exhausting, but we believe that everything becomes easier with a little data! Today we released the Wolfram Travel Assistant App, another in our line of Wolfram|Alpha-powered iOS apps. Whether you need help during trip planning or while currently on a vacation, this app is a great addition to your itinerary!
In my last blog post on plotting functionality in Wolfram|Alpha, we looked at 2D and 3D Cartesian plotting. In this post, we will look at 2D polar and parametric plotting.
For those of you unfamiliar with polar plots, a point on a plane in polar coordinates is located by determining an angle θ and a radius r. For example, the Cartesian point (x, y) = (1, 1) has the polar coordinates (r, θ) = (√2,π/4). The following diagram illustrates the relationship between Cartesian and polar plots.

To generate a polar plot, we need to specify a function that, given an angle θ, returns a radius r that is a function r(θ). Making a polar plot in Wolfram|Alpha is very easy; for example, we can plot Archimedes’ spiral. More »
 10
10
It seems the sun won’t let up this summer, with many parts of the United States experiencing record-level temperatures. With the excessive heat comes the danger of overexposure to the sun, but it’s often hard to know you’re at risk until it’s too late. The newly released Wolfram Sun Exposure Reference App for iOS can aid in calculating just how much sun is too much and can offer recommendations on which SPF level to apply.