8
8
It is immediately clear to anyone who has used the site that Wolfram|Alpha knows a lot about mathematics. When computing integrals, sums, statistics, properties of mathematical objects, or a myriad of other mathematical and mathematics-related problems, it typically returns an extensive and exhaustively complete result. Which is of course not surprising, given that Wolfram|Alpha has the entire power and knowledge of Mathematica behind it, especially when combined with the fact that this native “smarts” is further augmented with large amounts of curated data and customized processing.
However, many visitors to the site have noted in the past that Wolfram|Alpha had relatively little computable knowledge about mathematical terms themselves, a state of affairs in contrast to its knowledge of words in the English language, and perhaps surprising in light of the existence of another Wolfram site devoted to the definition and description of terms in mathematics, namely MathWorld.
As readers of MathWorld likely already know, the entire MathWorld website is written and built using Mathematica. It has therefore been possible to programmatically process the entire 13,000+ entries comprising MathWorld into the native data format of Wolfram|Alpha, thus exposing its content in more computable form.
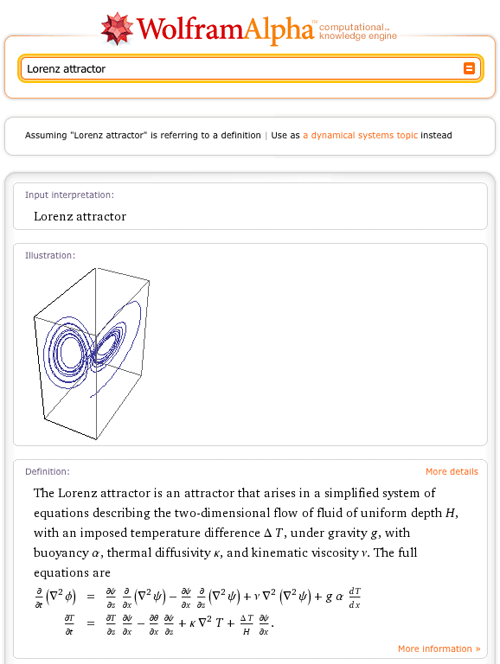
As an example of the sort of new knowledge this confluence brings to Wolfram|Alpha, consider the input “Lorenz attractor”. In the past, this would simply bring up a Wolfram|Alpha future topic page.
With the incorporation of MathWorld content, the default parse now goes to a description of the attractor, complete with an illustrative figure and some helpful typeset equations:
 5
5
When we are growing up and learning about the world, there are moments when a topic or idea really catches our attention. Perhaps it is while reading a book or during a lecture given by a good teacher. For me, one of those moments occurred during my junior year of high school in Mr. Brooks’s chemistry class. We were learning about the structure of the atom, and Mr. Brooks did a demonstration for us. He turned off the lights in the classroom and turned on a hydrogen discharge tube. The tube glowed with a pink light. Then Mr. Brooks put a prism in front of the glowing discharge tube, and several vertical lines of light appeared on the chalk board behind the prism.
At the time, I didn’t really understand that the voltage applied across the discharge tube was exciting the electrons around the hydrogen atoms and that the lines formed as the pink light passed through the prism were characteristic wavelengths of light being emitted as the electrons around the hydrogen atoms returned to lower energy levels. But I clearly remember the intense curiosity I felt about the phenomenon I was witnessing. It is, therefore, with some nostalgia that I announce the addition of the National Institute of Standards and Technology’s (NIST) atomic spectra database to Wolfram|Alpha.
Investigation of atomic spectra contributed significantly to our understanding of atomic structure and are described by the Rydberg formula. Furthermore, atomic spectra are used by astronomers to classify and determine the composition of stars. Today, the NIST database has become the most comprehensive and reliable set of data for atomic spectra and includes information about spectral lines and atomic energy levels associated with many elements and ions. All of this data can now be found in Wolfram|Alpha, including that visible hydrogen spectrum I was so curious about in high school:
 11
11
Wolfram|Alpha is making possible a whole new very interesting and very powerful kind of computing. And with the release today of version 2.0 of the Wolfram|Alpha API, it’s going to be considerably easier for a broad range of software developers to take advantage of it.
I’m happy to say that it seems as if Wolfram|Alpha is pretty useful to humans—for example through the wolframalpha.com website. But it also turns out that Wolfram|Alpha is extremely useful to programs. And in fact, even today, the number of requests coming to Wolfram|Alpha each second from programs often exceeds by some margin all the requests coming directly from humans.
The reason for this popularity is really pretty simple: Wolfram|Alpha completely changes the economics of a lot of programming. You see, these days a remarkable number of programs rely on having some kind of knowledge. And traditionally, the only way to get knowledge into a program was for the programmer to painstakingly put it there.
But with Wolfram|Alpha in the picture, it’s a different story. Because built into Wolfram|Alpha is already a huge amount of computable knowledge. And if a program is connected to Wolfram|Alpha, then it can immediately make use of all that knowledge.
Whether one’s building a website or a mobile app or desktop software or an enterprise application, the point is that one can use Wolfram|Alpha as a “knowledge-based computing” platform—so that having all sorts of computable knowledge becomes effectively free from an engineering point of view.
How does a program communicate with Wolfram|Alpha? It uses the Wolfram|Alpha API. (These days, API is pretty much a term on its own, but it comes from “Application Program Interface”.)
More »
 9
9
As kids start to return to classes after the holidays, we’re happy to announce that Wolfram|Alpha has the ability to compute some interesting information about their school districts. You can now use Wolfram|Alpha to analyze and compare data on student-teacher ratios, expenditures, revenues, and salaries in more than 18,000 public school districts in the United States.
Let’s start with an example on the West Coast: Seattle Public Schools is one of the larger districts in the country, with over 100 schools and more than 45,000 students. The student-teacher ratio is 18:1, and if you scroll down you’ll see that total expenditures are about $14,000 per student per year.
 44
44
Today we’re releasing the first three of a planned series of “course assistant” apps, built using Wolfram|Alpha technology.


The long-term goal is to have an assistant app for every major course, from elementary school to graduate school. And the good news is that Wolfram|Alpha has the breadth and depth of capabilities to make this possible—and not only in traditionally “computational” kinds of courses.
The concept of these apps is to make it as quick and easy as possible to access the particular capabilities of Wolfram|Alpha relevant for specific courses. Each app is organized according to the major curriculum units of a course. Then within each section of the app, there are parts that cover each of the particular types of problems relevant to that unit.
More »
 7
7
Today we unveiled a new look on the wolframalpha.com site. We decided the website needed to be reorganized to allow expansion for upcoming consumer, enterprise, and developer products. 2011 is going to be an exciting year for Wolfram|Alpha!
When visiting the site you’ll notice an updated version of your home page. Once you’re there, “take a quick tour”, visit the newly redesigned product pages, and explore resources and tools.

You may have noticed that we’re developing new features on the results pages, too. One of those features is “linked results”. For example, enter a query for “Chicago”. Notice the blue underlined links? Click one to dig deeper into Wolfram|Alpha and see more related information.

We’re also developing “dog-ear peelbacks”. Hover over the dog-ear in the left corner of each pod to uncover how you can save the contents of the pod as an image or copyable plaintext.

The site’s new look is just the first of many new things to come here at Wolfram|Alpha. We’re looking forward to sharing them with you!
 2
2
Today we’re officially wrapping up Wolfram|Alpha’s Deck the Halls with Facts & Knowledge Holiday Gift-Away by re-opening the gallery and announcing the winners! In early December we launched the contest as a way to say thank you for making 2010 a great year for Wolfram|Alpha, and to give some fun Wolfram swag to members of our community.
To start, we gifted Wolfram|Alpha Spikey paper sculpture kits to the first 500 people to enter the contest by submitting their favorite Wolfram|Alpha fun facts. We enjoyed reading all of the clever fun facts contestants uncovered in Wolfram|Alpha. Nyth discovered that eating a serving of bacon a day for one year will result in the consumption of 2.5lbs of fat. Sri found that the average life expectancy of a tortoise is 137 years. You can dive into Wolfram|Alpha to discover a countless number of fun facts.
Contestants had the opportunity to enter photos of their Wolfram|Alpha Spikeys, along with their fun facts, in a vote-off for a chance to win prizes such as Mathematica Professional, an iPad, Wolfram mobile apps, and T-shirts. The votes have been tallied and the winners have been announced on the Holiday Gift-Away site. Congratulations to all of the winners.
Online voting contests have their share of challenges. During the vote-off we discovered a few vulnerabilities in the voting system. We put additional measures in place to help secure voting, and we promptly identified and removed votes that fell outside of the contest’s rules. Once voting closed, we conducted a second round of auditing. It was very important to us that we reviewed the data and confirmed the correct winners.
Thank you to everyone who submitted their favorite Wolfram|Alpha fun facts and Spikey photos and supported their favorite entries in the vote-off!
 3
3
The real line runs from negative to positive infinity and consists of rational and irrational numbers. It generally appears horizontally, and every point corresponds to a real number. Also known as a number line in school, the real line is said to be one of the most useful ways to understand basic mathematics. Wolfram|Alpha can now aid you in learning the difference between x<-5 and x>5, or Abs[x]<2.
Wolfram|Alpha now graphs inequalities and points on the real line. This new feature in Wolfram|Alpha allows you to plot a single inequality or a list of multiple inequalities. Let’s start off simply and try “number line x<100”.
You can easily see that this is the set of all real numbers from negative infinity to, but not including, 100.
What if you need to plot a more difficult inequality, like “number line 3x<7x^2+2”? This plot will show that the solutions to this inequality are all real numbers between negative and positive infinity.
More »
 4
4
Consider packing circles inside a circular container, or less abstractly, placing cookie dough on a cookie sheet. In the case of cookies, which expand to be a roughly circular shape, you don’t want them so close that they run into each other. At the same time, you don’t want them too far apart, because that would mean fewer cookies.
One of the latest features of Wolfram|Alpha is the ability to get information about packing circles into circles.
For instance, suppose you have a circular baking sheet with a diameter of 12 inches, and you want to make 20 cookies. You can ask Wolfram|Alpha “pack 20 circles in a diameter 12 inch circle”; not only does it give you a diagram of the densest packing, but also the largest radius of the circular cookies on the 12-inch baking sheet.
Or you might know the size of the cookies and want to know how many can fit? One way to get the answer would be “pack r=1 circles in a diameter 12 circle”.
More »