The Top 100+ Sines of Wolfram|Alpha

While Wolfram|Alpha can do many sorts of computations, mathematical calculations are one of its particular specialties. In fact, using the power of Mathematica‘s computational capabilities under the hood, Wolfram|Alpha can do many things, ranging from the very simple to the fiendishly complicated, with mathematical functions.

To highlight what we mean by “many” (and we do indeed mean it), let’s take the unassuming sine function as an example. Here is a list that started out as 93 possibilities of what Wolfram|Alpha can do with sine (one for each day of summer), but ended up including a number of bonus inputs above and beyond that which we couldn’t resist throwing in.

Let’s start with the simple input sin(x) for the function itself:

For those who know about such things, most of the results above apply to real values of the argument x. If on the other hand you use a different form of the argument such as sin(z) or sin(x + i y), Wolfram|Alpha will prefer an interpretation assuming complex variables, and so give a different set of plots and results:

Of course, one can request each of the above computational results individually, for example, global maxima sin(x). One can also generate a multitude of plots by specifically asking for them, including:

• Plot sin(x), sin(2x), sin(3x)
• Plot sin(x), sin(sin(x)), sin(sin(sin(x))), sin(sin(sin(sin(x)))), sin(sin(sin(sin(sin(x)))))
• Contourplot sin(x/|y| – y/|x|) from x = -pi to pi and y = -pi to pi
• Plot3d sin(x – y) / sin(x + y) from x = -2pi to 2pi and y = -2pi to 2pi
• Polar plot r = 1 + sin(100 theta)

One can also easily plot more complicated expressions of the sine function, such as:

• Plot frac(1/frac(1/sin(x)))
• Plot sin (x!)! from x = -3 to 3
• Plot nestlist(sin, 1., 100)
• Parametric plot {max(sin(t), cos(pi t)), max(cos(t), sin(pi t))} from t = 0 to 100
• Plot3d sin(sin(x + i y)) from x =-pi to pi and y =-pi to pi
• Polar plot min(sin(x), sin(sqrt(2) x), sin(sqrt(3) x), sin(sqrt(5) x)) from x = 0 to 100 pi
• Polar plot r = exp(sin(theta)) – 2 cos(4 theta) + sin^5(theta/12 – pi/24)
• Parametric plot3D {sin(s + pi/2) + sin(s + pi/2)sin (t + pi/2)/2, sin(s) + sin(s)sin (t + pi/2)/2, sin (t)/2} from s = 0 to 2pi and t = 0 to 2pi

And even many functions using literal Mathematica syntax, such as:

• StreamDensityPlot[{Re[Sin[x + I y]], Im[Sin[x + I y]]}, {x, -Pi, Pi}, {y, -Pi, Pi}, ColorFunction -> “ThermometerColors”]
• Plot[Table[Sin[k x], {k, 0, 30}],{x, 0, Pi/2}] in purple

One can calculate special values of the sine function, such as sin(pi/88). Conversely, given the resulting value 0.0356923338389804557600…

…one can recognize it as a value of the sine function at x = pi/88 (the first of the three possible closed forms returned as shown above). So motivated, one might consider asking for a list of all special values at once using the input special values of sin(x). A particularly beautiful example in this class is function expand sin(pi/17), which shows the classic result that Gauss found on his 17th birthday.

One can ask for special forms of values and properties of values directly:

• Is sin(2/3) algebraic?
• Toradicals(sin(pi/(2^4 3 5)))

Find periods:

• Period of sin(x)
• Period of sin(x) + 2sin(2x) + 3sin(3x)

And find minima and maxima of functions containing sine:

• Minimize sinx + |x|
• Maximize (sin(x)/x)^2 between pi and 4 pi

One can draw 2D and 3D Lissajous figures:

• Parametric plot {sin(11t), sin(13t)}
• Parametric plot {sin(2t), sin(3t), sin(5t)} from t = 0 to 2pi

And get their curvatures:

• Curvature of {sin(3t), sin(4t)} at t = 1

One can ask for inflection points:

• Inflection points sin(x)

Arc lengths:

• Arc length {sin(t), sin(2t)} from t = 0 to pi
• Arc length r = phi sin(phi) from phi = 0 to 12pi

Corners:

• Corners |sin(x)|

And periodicity:

• Periodicity sin(4x + pi/3)

There are a multitude of mathematical formulas that can be requested. For concrete cases, consider:

• Trig reduce sin(x)^10
• Trig expand sin(10x)

As well as general formulas:

• Half-angle formulas sinx
• Double-angle formulas sinx
• Addition formulas sinx

Wolfram|Alpha also knows about many specific kinds of representations:

• Product representations sinx
• Limit representations sinx
• Sinx in terms of hypergeometrics

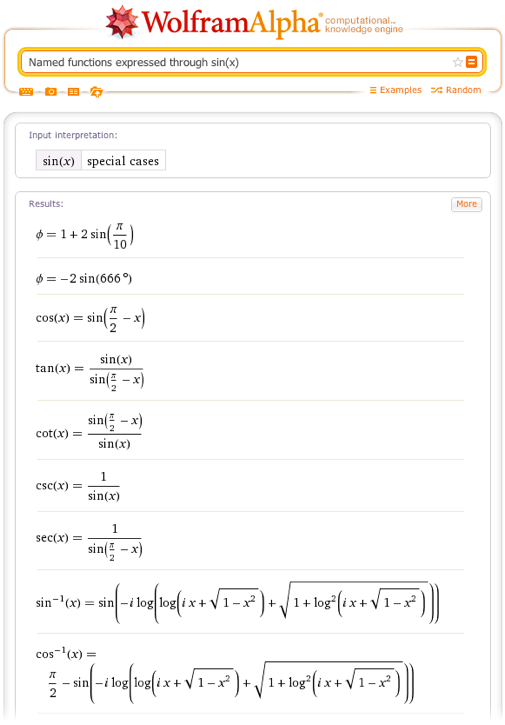
One can ask for the relation of the sine functions with other functions:

• Sinx in exponentials
• Relations between sin(x), cos(x)
• Relations between sinx, tanx

Including its relation with the inverse function and other functions expressed in terms of sine:

• Relations with inverse function sinx
• Named functions expressed through sin(x)

One can solve equations containing the sine functions:

• Find all solutions for cosx + sinx = tanx
• Solve cos(x) > 2sin(x)

Prove trigonometric identities involving the sine function:

• Verify: sin(x + y) sin(x – y) = sin^2x – sin^2y

Find discontinuities and poles of expressions containing sine:

• Discontinuities x / sin(x)
• Poles x / sin(x)

Differentiate the sine function:

• Sixth derivative of x sin(2^x) at x = 0
• d^n / dx^n sin(x)

Carry out sums:

• Sum sin(kx) for k = 1 to n

And, of course, integrate functions of sine:

• Integrate sin(x) dx from x = 0 to pi
• Integrate sin(x^3)^3 dx
• Integrate by parts cos^2(x) sin^4(x)
• Root mean square sin(4x+pi/3)

One can get sample lists of sums, products, and integrals:

• Finite sums containing sin(x)
• Infinite sums containing sinx
• Products containing sinx
• Indefinite integrals containing sinx
• Definite integrals containing sinx

Integral transforms:

• Fourier transform of sin(x)
• Laplace transform of sin(x)
• Hilbert transform of sin(x)

And find limits:

• Limit as x goes to 0 of ln(2 + sqrt(arctan(x)*sin(1/x)))
• Lim sin(x)/x as x -> 0

One can expand the sine function in a series:

• Series of sin(x) to order 10

Sum the Taylor series to finite order in closed form:

• Summed truncated Taylor series of sin(x)

Or get a Pade approximation of the sine function:

• [5/5] pade of sin(x)

One can simplify more complicated expressions involving sine:

• Simplify sin(2 arctan(3x) + pi)

And verify identities:

• Verify: sin(x + y)sin(x – y) = sin^2x – sin^2y

As well as expand a function into a Fourier sin series:

• Fourier sin series unitstep(x)

The sine function has many relatives and generalizations, including but not limited to:

• haversin(x)
• versin(x)
• qsin(x)

One can use the sine function in probability calculations, for example, to find the expectation for sin(x) assuming x is distributed normally:

• E(sin(x)) where x ~ N(0,1)

One can solve differential equations involving the sine function:

• y‘ + sinx y = 0
• y” – 1/3 y‘ + sin x y^3 = 0
• cos(x) dx + sin(y) dy = 0

Calculate Wronskians involving the sine functions:

• Wronskian({cos(x), sin(x)}, x)

And find the differential equation obeyed by an expression containing the sine function:

• Differential equation for sin(x^p)

One can use the sine law and the spherical law of sines:

• sine law calculator
• spherical law of sines

Express and approximate the value of pi through values of the sine function:

• Express 3.14 through sin(1) and sin(2)

And request an interactive version of the sine function:

• Vary b in Plot[a Sin[b x + c], {x, -3, 3}]

One can even do computations on URL-referenced objects on the internet, for example, providing analysis of an image of a sine function taken from The Wolfram Functions Site:

• Analyze http://wolfr.am/OA39R2

Last, not least, one can “play” the sine function:

• Play sin(440 t)

We could go on (and on, and on), but that almost certainly suffices (“many” indeed). So as many of you are going back to school after what we hope was an enjoyable summer, please keep Wolfram|Alpha and its powerful collection of functionality in mind as you resume your studies. While we realize not everyone will enjoy getting back into the academic term as much as they did the allegedly halcyon days of summer, we hope there are at least a few of you out there who will have more fun learning with the help of Wolfram|Alpha, now that you know about it, than you did during your long, boring summer. 🙂