8
8
In recent dinner conversation with my brother, I commented that I was “99.9 repeating” percent sure that my favorite author, Jorge Luis Borges, had lived into the 1980s (Wolfram|Alpha later showed me that he did, in fact, live through 1986!). I felt confident about my knowledge, but wanted to leave myself a little wiggle room, just in case. My brother grinned at me and said, “I know you know your geometric sequences. If you say you’re 99.9 repeating percent sure, then you’re 100 percent sure.”
I blushed, embarrassed. He was definitely right!
But just what did my brother mean? Well, he reminded me that:
99.999… = 99 + 9/10 + 9/100 + 9/1000 + 9/10000…
Glancing at the above, the series 9/10 + 9/100 + 9/1000 + 9/10000… stands out. Each term in this series is 1/10 times the term before it, making it a geometric series. A geometric series is a series wherein each term in the sequence is a constant number, r, multiplied by the term before it. Any geometric series whose r satisfies -1 < r < 1 is a convergent series, and we can say to what the series converges:
Sum[r^k, {k, 0, ∞}] = 1/(1-r)
 3
3
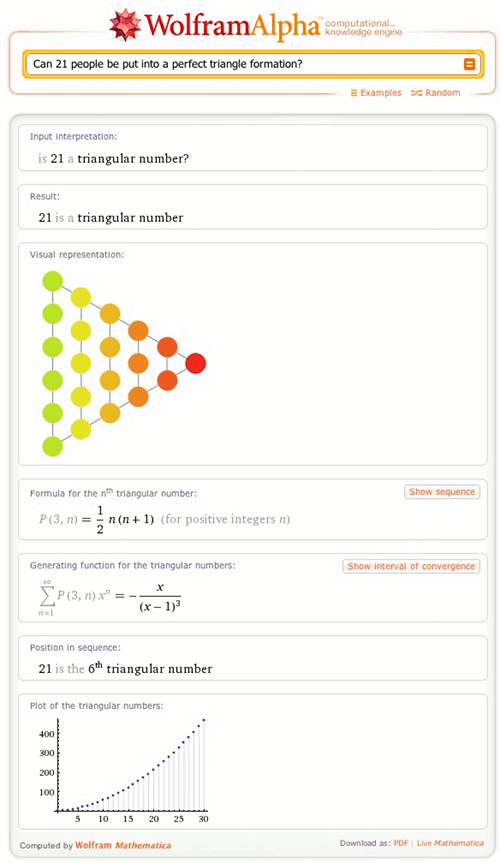
Want to know if you and your 20 teammates can march in perfect triangular formation in a parade? Or maybe you want to know how many glasses you’ll need in order to break the world record for largest champagne pyramid (currently 60 stories high, with 37,820 glasses).
Whether you’re stacking watermelons or water-skiers or just playing with dots on paper, if you want to make a perfect geometrical formation, then you’re interested in “figurate” numbers. These are numbers for which that number of things can be arranged into a perfect geometrical shape, such as a triangle (in the case of the “triangular numbers”) or a triangular pyramid (AKA, a tetrahedron), which is the shape of champagne pyramids.
Wolfram|Alpha now has the ability to tell you if a given number is any figurate number. Entering our first question, “Can 21 people be put into a perfect triangle formation?”, into Wolfram|Alpha gives an affirmative, along with a diagram and other useful information:
 3
3
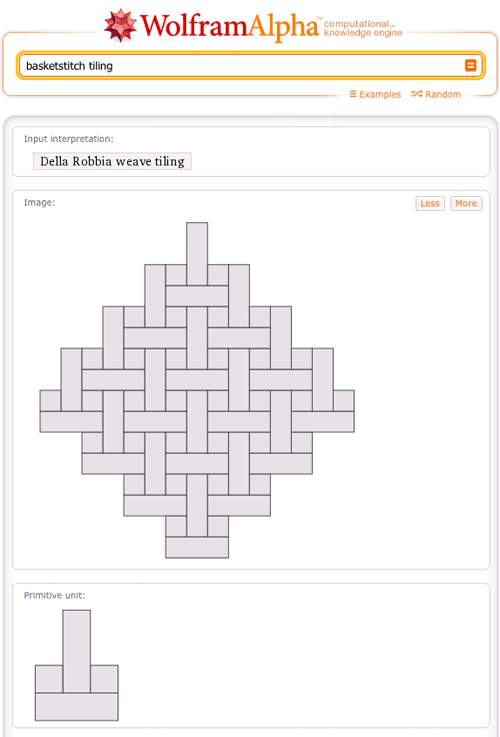
Periodic tilings (also known as tessellations) are often beautiful arrangements of one or more shapes, known as tiles, into regular patterns, which if extended infinitely are capable of covering the entire plane without gaps. Wolfram|Alpha has possessed detailed knowledge on more than 50 common (and uncommon) varieties of periodic tilings for some time, as illustrated, for example, in the case of the basketstitch tiling:
Periodic tilings possess an individual motif (more formally known as a primitive unit) that is repeated iteratively in a predictable (periodic) way. Such tilings are therefore intimately related to the set of symmetry groups of the plane, known as wallpaper groups. While the most general set of geometric similarity (i.e., shape-preserving) operations in the plane includes rotation (change in angle), dilation/expansion (change in size), reflection (flipping about an axis), and translation (change in position), only translation is needed to produce a periodic tiling from a correctly constructed primitive unit. More »
 5
5
On a moonlit stroll, a young man points to the cloudless sky and says, “Look—a full moon!”
His date is not impressed. “Technically,” she replies, “the Moon’s not full until 2pm, when its ecliptic longitude is opposite to that of the Sun.”
Hoping to save his pride, he replies, “But the Moon looks completely illuminated.”
“It’s never one hundred percent illuminated,” his date says, unfazed. She’s a tough cookie. “Oh, and on this side of the world it’ll be a corn moon.”
Pretending to check his watch, the young man gets confused. He remembers his science teacher explaining that the Moon reflects sunlight and that it is full when it is on the other side of the Earth from the sun, but the nighttime half of the Earth is on the opposite side of the Sun, so how could that be 2pm? Did the newspaper say it would be a full moon tonight, or did it say tomorrow night? And what’s a corn moon?
There’s only one thing he can do: look it up on Wolfram|Alpha!
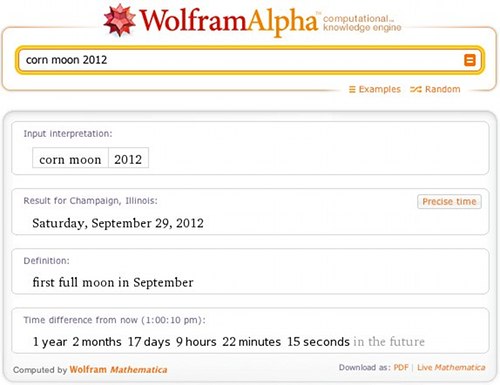
One of the latest features added to Wolfram|Alpha is more coverage of full moons and other Moon phases. Back when people got their information from only a local newspaper, it was relatively simple to say that one night or another would be a full moon, because for a specific location, the time of a full moon would be closest to midnight on that day. But now it is easy to get your information from a newspaper that is far away, so its date can be off by a day. Of course, Wolfram|Alpha detects your location, so it is able to predict the date of the next full moon in your area, and the “Precise time” button reveals the exact time the full moon will take place.
Remember that because of time zone differences, there is always part of the world that is on a different day. And that affects labels like “corn moon”, which is the first full moon in September. The beginning and ending dates of September depend on the time zone, and sometimes the full moon is close to this boundary. The next ambiguous corn moon will be in 2012. More »
 8
8
Today we are pleased to unveil the Wolfram Genealogy & History Research Assistant and the Wolfram Personal Finance Assistant Apps for iOS! These new additions to Wolfram’s wide offering of specialized apps are the first in our series of Personal Assistant Apps, which use Wolfram’s vast knowledge base to enrich topics that matter most to you. Explore the world of your ancestors with the Wolfram Genealogy & History Research Assistant, the only tool that lets you discover what was going on while they lived. Map family relations and expand on what you already know about any of your ancestors with a simple, easy-to-use interface. It’s as if you’re traveling through time with the tips of your fingers.
 One way you can use the Wolfram Genealogy & History Research Assistant is to track the name popularity of your family members using the app’s specialized menus. More »
One way you can use the Wolfram Genealogy & History Research Assistant is to track the name popularity of your family members using the app’s specialized menus. More »
 7
7
For thousands of years, people have been making music: banging, blowing, bowing, and strumming away as soloists or in groups. With music being an integral part of culture, it is not hard to imagine that the invention and evolution of various musical instruments is a key indicator of human ingenuity. Each instrument is unique, its physical and sonic characteristics often emblematic of the culture from which it emanates.
Wolfram|Alpha now provides a significant amount of information about a myriad of musical instruments. Ask Wolfram|Alpha about any set of instruments to get a side-by-side comparison of parameters and characteristics.
For many instruments, you will notice two pods for range: “Written range” and “Sounding range”. This is because in standard music notation, some instruments are written differently than they sound; these are called transposing instruments. In many ways, it is a terribly confusing notion. A score displays a certain pitch, but the pitch the instrument produces may be higher or lower. Wolfram|Alpha illustrates this difference by displaying the pitch range (along with the corresponding frequencies and keys on a piano keyboard) for how the instrument is written as well as how it sounds. For example, the flute is a non-transposing instrument and is “written as sounds”. However, its close cousin, the alto flute, sounds a perfect fourth lower than written. Still unclear? Click the “play alto flute range notes” in the written range and sounding range pods to hear the difference. Or, you can ask Wolfram|Alpha to give you the interval between the bottom note of the written range and the corresponding sounding note by querying “interval of C4 and G3“.
 1
1
A few weeks ago, we pointed out some new additions to Wolfram|Alpha from the World Bank’s World Development Indicators database, primarily focused on labor and employment around the world. We’ve also incorporated data about doing business in most countries, collected by a World Bank project called, appropriately, “Doing Business”.
This data covers a wide range of issues, including import/export costs, business tax rates, and the time required to complete various business-related activities. Try the following examples to get a better sense of the breadth of this dataset:
- Export costs in Brazil vs. Argentina »
- New businesses registered in Japan vs. India »
- Credit bureau coverage in Asia »
- Europe total business tax rate »
- How much does it cost to start a business in India, Mexico, Singapore »
- Time required to start a business »
Wolfram|Alpha can also rank countries according to a number of business-related indices. Ask about the ease of doing business in Eurozone countries, for example, and you’ll see that Ireland and Greece occupy the ends of this spectrum. In this case, a higher index score indicates a regulatory environment that is generally unfriendly to business operation; in light of Greece’s recent economic woes, it should come as no surprise to see that country at the bottom of the list. (Note that for all the properties in this dataset, you can click the “Definition” button in the input interpretation or in other pods to get more details on each property.)
 3
3
The warm summer weather provides a great opportunity to explore a new city on foot! Using OpenStreetMaps in Wolfram|Alpha, you can map out computations and comparisons of some of the world’s most famous streets and explore places of interest.
Doing some shopping on Fifth Avenue? Walking the street for its entire length will take you 200 minutes! An African Burial Ground National Monument and Theodore Roosevelt’s birthplace are also within a mile of this route. If the trip is wearing you down, Bronx-Lebanon Hospital is only 2 miles away. More »