A new school year is here, and many students are diving into new levels of math. Fortunately, this year, you have Wolfram|Alpha to help you work through math problems and understand new concepts. Wolfram|Alpha contains information from the most basic math problems to advanced and even research-level mathematics. If you are not yet aware of Wolfram|Alpha’s math capabilities, you are about to have a “wow” moment. For the Wolfram|Alpha veterans, we have added many math features since the end of the last school year. In this post, we’re highlighting some existing Wolfram|Alpha math essentials, such as adding fractions, solving equations, statistics, and examples from new topics areas like cusps and corners, stationary points, asymptotes, and geometry.

You can access the computational power of Wolfram|Alpha through the free website, via Wolfram|Alpha Widgets, with the Wolfram|Alpha App for iPhone, iPod touch, and the iPad! Even better, the Wolfram|Alpha Apps for iPhone, and iPod touch, and the iPad are now on sale in the App Store for $0.99 though September 12.

If you need to brush up on adding fractions, solving equations, or finding a derivative, Wolfram|Alpha is the place to go. Wolfram|Alpha not only has the ability to find the solutions to these math problems, but also to show one way of reaching the solution with the “Show Steps” button. Check out the post “Step-by-Step Math” for more on this feature.

You can find this widget, and many others, in the Wolfram|Alpha Widget Gallery. Customize or build your own to help you work through common math problems. Then add these widgets to your website or blog, and share them with friends on Facebook and other social networks.

Of course, Wolfram|Alpha also covers statistics and probability. For example, Wolfram|Alpha can compute coin tossing probabilities such as “probability of 21 coin tosses“, and provides information on normal distribution: More »

Wolfram|Alpha computes things. While the use of computations to predict the outcomes of scientific experiments, natural processes, and mathematical operations is by no means new (it has become a ubiquitous tool over the last few hundred years), the ease of use and accessibility of a large, powerful, and ever-expanding collection of such computations provided by Wolfram|Alpha is.

Virtually all known processes occur in such a way that certain functionals that describe them become extremal. Typically this happens with the action for time dependent processes and quantities such as the free energy for static configurations. The equations describing the extremality condition of a functional are frequently low-order ordinary and/or partial differential equations and their solutions. For example, for a pendulum: Frechet derivative of Integrate[x'[t]^2/2 – Cos[x[t]], {t, -inf, inf}] wrt x[tau]. Unfortunately, if one uses a sufficiently realistic physical model that incorporates all potentially relevant variables (including things like friction, temperature dependence, deformation, and so forth), the resulting equations typically become complicated—so much so that in most cases, no exact closed-form solution can be found, meaning the equations must be solved using numerical techniques. A simple example is provided by free fall from large heights:

On the other hand, some systems, such as the force of a simple spring, can be described by formulas involving simple low-order polynomial or rational relations between the relevant problem variables (in this case, Hooke’s law, F = k x):

Over the last 200+ years, mathematicians and physicists have found a large, fascinating, and insightful world of phenomena that can be described exactly using these so-called special functions (also commonly known as “the special functions of mathematical physics”), the class of functions that describe phenomena between being difficult and complicated. It includes a few hundred members, and can be viewed as an extension of the so-called elementary functions such as exp(z), log(z), the trigonometric functions, their inverses, and related functions.

Special functions turn up in diverse areas ranging from the spherical pendulum in mechanics to inequivalent representations in quantum field theory, and most of them are solutions of first- or second-order ordinary differential equations. Textbooks often contain simple formulas that correspond to a simplified version of a general physical system—sometimes even without explicitly stating the implicit simplifying assumptions! However, it is often possible to give a more precise and correct result in terms of special functions. For instance, many physics textbooks offer a simple formula for the inductance of a circular coil with a small radius:

While Wolfram|Alpha knows (and allows you to compute with) this simple formula, it also knows the correct general result. In fact, if you just ask Wolfram|Alpha for inductance circular coil, you will be simultaneously presented with two calculators: the one you know from your electromagnetics textbook (small-radius approximation) and the fully correct one. And not only can you compute the results both ways (and see that the results do differ slightly for the chosen parameters, but that the difference can get arbitrarily large), you can also click on the second “Show formula” link (near the bottom of the page on the right side) to see the exact result—which, as can be seen, contains two sorts of special functions, denoted E(m) and K(m) and known as elliptic integrals: More »

Version 1.1 of the Wolfram|Alpha App for the iPhone & iPod is now available in the App Store. The new version includes a number of new features that continue to improve the app’s unique mobile Wolfram|Alpha experience. Perhaps its most iconic feature, the specialized keyboards that greet you when you first open the Wolfram|Alpha App, have been painstakingly constructed to ease the burden of entering queries, whether you’re converting from pounds to euros or computing a numerical value for the Weierstrass p-function . Our goal in creating these keyboards was to form families of characters that naturally occur together both in common use and in traditional mathematical applications. We also wanted mathematical expressions to look and feel natural to enhance usability and understanding. Version 1.1 has four specialized keyboards: the default keyboard, the “math” keyboard accessed by the right-shift key  , the “Greek” keyboard accessed by one press of the left-shift key , and the “symbol” keyboard accessed by a second press of the left-shift key.

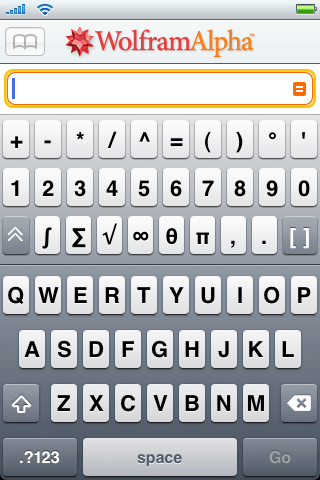
To determine the optimal keyboard layout, we scoured Wolfram|Alpha’s server logs for the most commonly entered phrases that have characters with meaning in Wolfram|Alpha. Given that Wolfram|Alpha is built on Mathematica, one of its core strengths is advanced mathematics. True to form most of the commonly typed characters are related to math. For example, you would generally type the word “integrate” to compute an integral on the Wolfram|Alpha website. In the Wolfram|Alpha App you could simply type the  key on the math keyboard. The same is true for other symbols common in math, such as and . Specifying geometric shapes, such as a triangle, is straightforward as well.

More »

July 17, 2019 Update: Step-by-step solutions has been updated! Learn more.

Have you ever given up working on a math problem because you couldn’t figure out the next step? Wolfram|Alpha can guide you step by step through the process of solving many mathematical problems, from solving a simple quadratic equation to taking the integral of a complex function.

When trying to find the roots of 3x²+x–7=4x, Wolfram|Alpha can break down the steps for you if you click the “Show steps” button in the Result pod.

As you can see, Wolfram|Alpha can find the roots of quadratic equations. Wolfram|Alpha shows how to solve this equation by completing the square and then solving for x. Of course, there are other ways to solve this problem! More »