What do the following two math problems have in common?
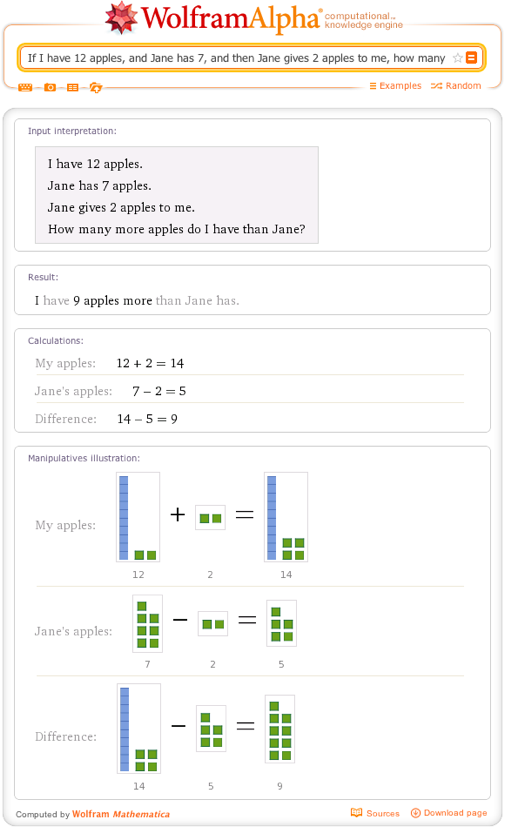
- If I have 12 apples, and Jane has 7, and then Jane gives 2 apples to me, how many more apples do I have than Jane?
- (12 + 2) – (7 – 2)
Answer: two things, actually. First, the two problems are essentially the same; the latter is just expressed in the language of symbolic mathematics. Second, Wolfram|Alpha can now solve both! That’s right, we’ve added math word problems to the kinds of questions you can ask Wolfram|Alpha!
Did you find the second problem easier? It’s no surprise that most people find “word problems” harder, or that the first step in solving them is to translate them into symbolic form. After all, this is why mathematical symbols were invented: to represent complex problems in a way that helps us organize our thinking in order to find their solutions.
Once expressed in symbols, solving a math problem is relatively easy. It can almost always be done by performing some purely mechanical process or “algorithm” (although it often helps to have a more intuitive understanding as well). Software programs like Mathematica know almost all these algorithms and can solve pretty much any symbolic problem you can think of.
But knowing how to solve symbolic math problems is like knowing how to use a saw to cut wood and a hammer to drive nails. You still can’t build a house unless you know where and when to use these tools. This is where Wolfram|Alpha can help.
Word problems are an important part of our mathematical education because real-life problems almost never present themselves to us in symbolic form. They are usually given in the form of a story, which we translate into symbolic math in order to solve. This is what Wolfram|Alpha does with elementary word problems: it not only gives you the answers, but it also helpfully translates the information in the problems into mathematical symbols, showing you the first (and most important) steps toward finding a solution.
Here’s what Wolfram|Alpha says if we enter the first problem: If I have 12 apples, and Jane has 7, and then Jane gives 2 apples to me, how many more apples do I have than Jane?
You can ask Wolfram|Alpha to solve any problem where people (or letters) have some common objects (like apples) and then gain, lose, or swap these objects. Wolfram|Alpha knows to ignore any irrelevant information and shows a calculation and illustration to help you understand how the numbers in the problem were used to find the solution.
Here’s an example of a word problem that tries to distract you with lots of irrelevant information and disorganized phrasing: Veronica owns 12 cats and 17 dogs. Maurice had 16 dogs and sells 3 to Veronica. How many cats are there in all if Maurice owns 1 cat?
Besides gaining, losing, and transferring objects among various entities, you can also solve word problems involving comparisons. The common core standards have many examples, including this one: Lucy has 3 fewer apples than Julie. Lucy has 2 apples. How many apples does Julie have?

Word problems can have several comparisons, which can involve multiplication/division as well as addition/subtraction: John has 3 cookies more than Bill. Bill has half as many cookies as John. How many cookies does John have?
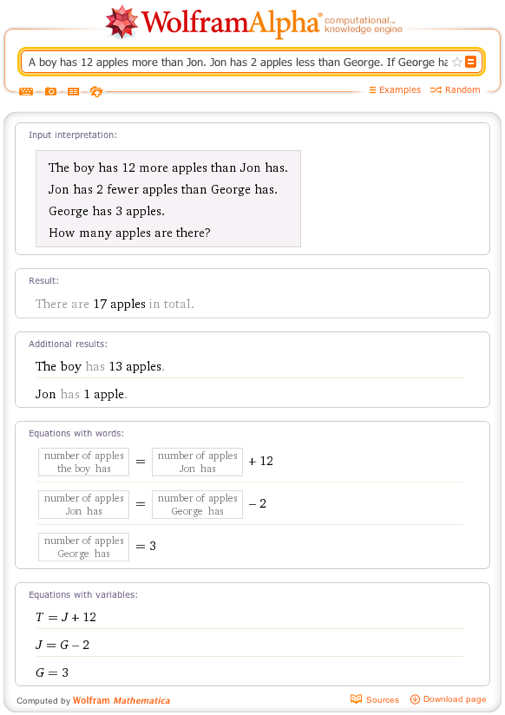
In addition to individual amounts and differences, Wolfram|Alpha can also tell you the total number of objects there are: A boy has 12 apples more than Jon. Jon has 2 apples less than George. If George has 3 apples, how many apples are there in all?
Not all word problems involve people. Wolfram|Alpha also understands simple arithmetic problems like this one: How many is 3 apples more than 2 apples?
There is an infinite variety of types of word problems, so of course, Wolfram|Alpha can’t cover all of them. However, we’ll be steadily improving the variety and difficulty of word problems that Wolfram|Alpha can solve, as well as enhancing the output. For example, we’ll soon be adding Step-by-step solutions to the systems of linear equations in the problems above.
We hope that students will use this feature to help them learn how to think through math word problems, which is one of the most challenging—and essential—parts of the elementary math curriculum.
What about rate problems, like “One train leaves the station at 3pm going 50 mph, and another train leaves at 4pm going 70mph. When do they meet?”
Hello Peter!
I am a Brazilian blogger, and constantly uses Wolfram Alpha ..
The features of Wolfram Alpha and its applications are becoming more refined.
I really liked your text and examples applied to this new functionality.
Hug!
Cutting-edge Natural Language Processing with a constant drive towards practical applications. Thanks for sharing and inspiring all of us!
Wow this is great. Can’t wait to see this expanded.
So it is not long until WolframAlpha can do all the logic puzzles on the LSAT and enter law school. That would be cool.
Something I’d definitely recommend adding: age comparison problems (for instance: “John is half Fred’s age. Fred is ten years older than John. How old is Fred?”). I remember having a lot of those types of word problems when I took that level of math.
This type of word problem is uneasy to solve because of confusions but WolframAlpha can solve it in a few moments.
Examples section is great for new users. I have started using WolframAlpha.
Are there plans to offer a rest API for Wolfram Alpha Pro?
Anastasia is with her father at the grocery store. She is wondering how much shopping is left. We have 70% of the items On our list. Her father said. Anastasia counts 14 items in the cart. How many grocery items are on the list.
let total items be x . 70% of x = 14 therefore , 0.7x = 14 , solve for x , get x = 20 .
Hi! Really nice! But what about joint work? For example “First machine do the job in 11 hours, second machine in 5 hours. How long will they work together?”
our boys each order their own small pizza, William eat 2/3 of his pizza. Mike east 2/5 of his pizza. Julio eats 1/2 of his pizza. Who ate the least amount of pizza
We want to know the average sugar content per packet in a brand of instant oatmeal. We consider a box of 18 packets which have an average of 12.2g of sugar per packet. The oatmeal factory did a more comprehensive study of there product and found that they have 13.1g sugar per packet.
1. Subjects=
2. Observations=
3. Sample size=
4. Perimeter=
5. Statistic=
Peter,
Can this be done in Mathematica 9. I am using it to teach my kids maths and this would be very helpful.
Yes, Pradeep, this can be done in Mathematica 9, via the Wolfram|Alpha integration.
Just enter “==” into a blank cell and then type freeform input !
What about this: I own a house in a school district that has a yearly budget of $100 million. How much of the budget will be funded by property taxes if the amount funded by state sales tax is $15 million and state income tax will be three times the amount funded by property taxes?
The weight of a half full tank is 302 pounds. Full the tank weighs 564 pounds. Find the weight of th empty vessel.
Can someone help me solve this right away
a swimming pool is formed by the intersection of two circles whose radii are both 9m. find the area of the swimming pool formed?e can anyone solve this right
I apologize that this is like a month late. It seemed like you needed the information really soon. Here’s the answer if you still want to know: 132.9 m^2
Hopefully that will be helpful to you.
A prescription was written for 270 tablets on the 14 of February. When does the prescription get run out if it is taken 4 times a day?
Its great to be here. I hope to gain and be a mathematician in future
The ratio of stocks declining in price to those advancing was 5 to 2. If 500,000 shares advanced, how many shares declined?
Where on this website can I write word problems to get help with answers?
Thank you for your question! You can ask word problem questions on the Wolfram|Alpha homepage at http://www.wolframalpha.com/.
Tyler has two savings accounts that his grandparents opened for him. One of the accounts pay 9% annual interest, whereas the other pays 11% annual interest. If you have $400 more invested at 11% than you invested at 9%, how much do you have invested in each account if the total amount of interest you earn in a year is $124?
Help! I am typing the word problem into WolframAlpha but it is not computing. Too many words? Or am I in the wrong area?
5 years ago, Daniel was older than Alex by 2 times. Now, both ages together, add up to 14 what are their ages now?
the football team scored 23 points last saterdaay
they scored a combination of 7 point touchdowns
and 3 point feild goals how many touchdowns
and how many field goals did they score
I need help with a word problem. if I could get it into a formula, I’d be able to solve it. I just need help getting it there.
The first pump is able to fill a tank of water in 15 minutes. The second pump can fill the same tank in 30 minutes. how long would it take to fill the tank if both pumps worked together?
ok. In a classroom there are 32 students total. Those students represent three different states. Arizona, texas, and OK. There were 8 more students from texas than from OK. There were nine fewer students from AZ than from OK. How many students were born in each state?
a heat engine operating between 1000°c and 25°c produce work that is entirely used up to run a refrigerating machine operating between 0°c – 25°c. calculate the ratio of the heat absorbed by the engine to that absorbed by the refrigerator assuming ideal operation for both
135 people need to drink some punch each glass holds 6 fl oz how many fl oz is needed to let everyone drink some
A merchant blends tea that sells for $4.10 a pound with tea that sells for $2.10 a pound to produce 60 lb of a mixture that sells for $3.30 a pound. How many pounds of each type of tea does the merchant use in the blend?
Using digits 1-9 are placed in the following three boxes, what box would the number 0 go.
Box one has 1,4,7
Box two has 2,5
Box three has 3,6,8,9
Digit sort problem?
The length of a rectangle is 4 ft longer than twice the width.If the perimeter is 68 ft, find the length and width of the rectangle.
Giovanni is visiting his grandmother who lives in a apartment building on the 25th floor. Giovanni enters the elevator in the lobby, which is the first floor in the building. The elevator stops on the 16th floor. What percentage of floors does Giovanni have left to reach his grandmothers floor?
I’m stuck with this question can anybody help me?
if a crayon is 8cm in length and 1cm in diameter and 5cm cubed. It’s a cylinder with a cone surmounted onto it what is the length and height
The larger of 2 numbers is 7 more than twice the smaller. Their sum is 34. Find the two numbers
a farme harvested 255 tonnes of crops. he sold of 15% of them. the crops that remained were 35% maize,20% beans and the rest sorghum. how many tonnes of sorghum was the farmer left with?
Thank you all for this rich list of new types of word problems. We are working on being able to process several other types of word problems, and this list has helped.
I’ll post here again once I’ve improved the range of this Wolfram|Alpha ability.
Thanks again,
Peter
William bought fourteen bags of cans that had a total price of $46.24.
He bought some bags of candy for $2.93 each and the rest for $3.51
Each. How many bags of $2.93 candy did William buy?
A -1.5 charge experiences a force of magnitude 500N at an angle of 110 counterclockwise from the x-axis. what are the X and Y components of the electric field in its vicinity
Biologists tagged 138 fish in a lake on january 1. On february 1 they returned and collected a random sample of 30 fish, 10 of which had been previously tagged. On the basis of this experiment, approximately how many fish does the lake have?
if a video game is £27 and then reduced to £22.50. by what fraction is it reduced by?
An agriculture company has 80 tons of type I fertilizer and 120 tons of type II fertilizer. The company mixes these fertilizer into two products. Product X requires 2 parts of type I and 1 part of type II fertilizers. Product Y requires 1 part of type I and 3 parts of type II fertilizers. If each product sells for $2000, what is the maximum revenue and how many of each product should be made and sold to maximize revenue?
The ratio of brown tiles to tan tiles is 2 to 3. If an artist needs 16 brown tiles to complete a mosaic, how many total tiles will the artist need?
The refractive index of gases, like air, changes linearly with the pressure according to the equation: n=1+3.6315exp-7P ( n is refractive index and P is pressure in Torr). Suppose a laser light (450 nm) in a double slit experiment produces second bright fringe at 1.3 degrees in normal air pressure (760 Torr). Suddenly the air pressure changes and the third bright fringe forms at the same angle. By how much did the pressure changed? The slit diatance is 2mm
I have tried to work this out does someone know what the answer is this this
If a cylinder has a volume428cm3 power of and a radius of 6 cm, how tall is it?
i need help!!!
A house painter was mixing up different colors to paint his own house. He mixed 3 liters of red paint with 2 liters of blue paint to create purple. He painted his living room with 2,500 ml of paint. He painted his bedroom with 1,500 ml. How many milliliters of paint were left over after the house painter finished those two rooms?
Hello! I use Wolfram Alpha very often. 😉 I am extremely excited for this!
a community organization had a member reduction and lost 1/9 of it’s members. of 176 were left after the reduction, how many members were there initially
What about minimum/maximum related word problems? Does anyone know if Wolfram Alpha can solve them?



 Comments Off
Comments Off