Connecting Music and Math with Wolfram|Alpha

While mathematics and music are inextricably linked, music is often regarded as magical. It transcends emotion and nature in a way that is often hard, if not impossible, to properly explain. For example, many people are deeply affected by the emotional power of Beethoven’s Ninth Symphony, but may not fully understand why. Perhaps great composers simply intuit mathematical connections to music.

But even music has plenty of structures that are clearly identifiable and thus computable. At Wolfram|Alpha, we are working hard to identify these underlying structures and are coming up with exciting ways to bring them to life.

Take a musical scale as an example. While we are used to arpeggios and melodic figures fluttering through familiar musical pieces, it is helpful to see that at its core, a scale has an intrinsic structure. Each pitch relates to the next by a certain measurable difference. Further, each of the pitches, which we perceive generally as high or low in a pitch space, has a specific frequency.

Or you can directly query the frequency of a given note:

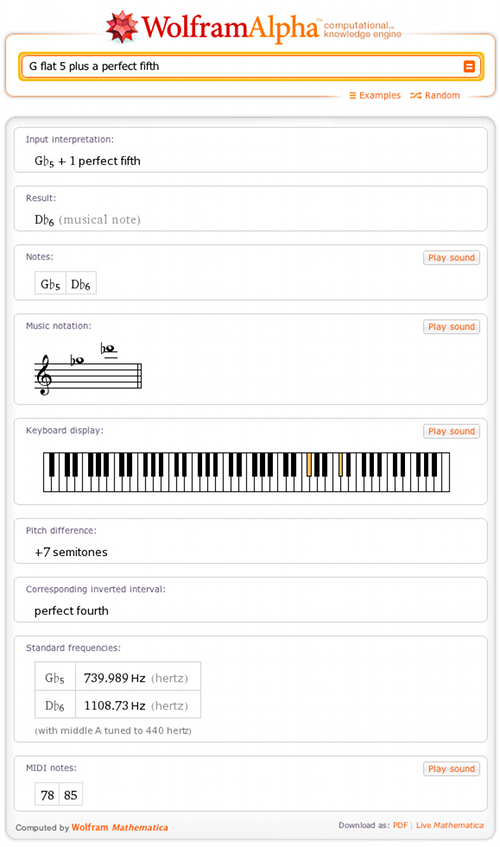
Or you can examine the properties of a given musical interval; Wolfram|Alpha provides support for music arithmetic, allowing users to get the result of a pitch plus or minus a given interval, such as a perfect fifth:

Wolfram|Alpha can also be used as a compositional tool. Perhaps you are not sure which scales contain a certain set of notes, or maybe you want to explore several scales that contain the same notes. We can do so simply by entering in several note names and computing the results. Wolfram|Alpha will return which scales and common chords contain those notes. Click on any of these to hear the result:

Musical styles and analytical techniques are constantly evolving. And at Wolfram|Alpha, we intend to cover as much as possible, from traditional tonal theory to more recent techniques of pitch-set analysis.

Enter one or more musical keys, for example, and Wolfram|Alpha will compute a number of useful facts, including closely related keys, the input keys’ position on the circle of fifths, and diatonic triads in a given key:

In the musical set theory example below, each pitch class is assigned a number with the convention that C = 0, C# = 1, D = 2, etc. Many theorists, such as Allen Forte, use this simple technique to classify various sets of pitches and apply transformations to them, as shown when you expand the results.

We hope that our efforts will help the greater community of both musicians and non-musicians alike, from pedagogy to composition itself. As the formal connection between math and music date back to the ancient Greeks, we have a lot of ground to cover and are excited about taking on the challenges of making it all computable: from Pythagoras, who was one of the first to observe that the different divisions of a string produced different harmonics, to modern pioneers of digital audio synthesis, like Max Mathews, who was one of the first to synthesize sounds using digital computers. We aim to leave no stone unturned.