2
2
Do you need to work with numbers that are of the magnitude of thousands, millions, or even billions? How about the thousandths, millionths, or billionths? Scientists and engineers need to work with really large and really small numbers every day. Now Wolfram|Alpha can help put all of those large and small numbers into scientific notation. For example, the Earth’s mass is about 5973600000000000000000000 kg, but it is nicely represented in scientific notation as 5.9736×10^24 kg.
 7
7
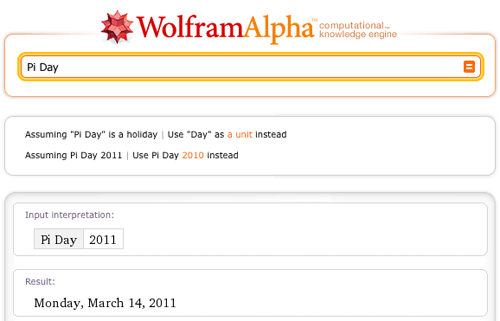
Yes, it is once again the time of the year when the mathematically inclined gather together to celebrate Pi Day…
…and, in the process, swap trivia of note on everyone’s (including Wolfram|Alpha’s) favorite number.
There have been no shortage of blog posts already written on the subject; see, for example, last year’s “Pi Day in Wolfram|Alpha” (or the Wolfram Blog Pi Day posts from 2008 or 2010). As already hinted at in last year’s blog, one would expect the pi to be ubiquitous in a computational knowledge engine—and so it is. Therefore, at the risk of beating a proven transcendental constant to death, this year we offer a few (well, OK: more than a few) additional pi-related esoterica courtesy of Wolfram|Alpha.
More »
 3
3
The real line runs from negative to positive infinity and consists of rational and irrational numbers. It generally appears horizontally, and every point corresponds to a real number. Also known as a number line in school, the real line is said to be one of the most useful ways to understand basic mathematics. Wolfram|Alpha can now aid you in learning the difference between x<-5 and x>5, or Abs[x]<2.
Wolfram|Alpha now graphs inequalities and points on the real line. This new feature in Wolfram|Alpha allows you to plot a single inequality or a list of multiple inequalities. Let’s start off simply and try “number line x<100”.
You can easily see that this is the set of all real numbers from negative infinity to, but not including, 100.
What if you need to plot a more difficult inequality, like “number line 3x<7x^2+2”? This plot will show that the solutions to this inequality are all real numbers between negative and positive infinity.
More »