Bonding is pretty fundamental, as it determines the shape of a molecule, which in turn determines how a molecule behaves. Wolfram|Alpha now supports Lewis structures—diagrams that show both the bonded and unbonded electrons in a molecule. But as any good teacher will tell you, even more important than finding the answer is the procedure used to get that answer. Thus, Wolfram|Alpha is expanding its Step-by-step interface into the realm of chemical bonding (with even more Step-by-step functionality coming soon).
Molecules are composed of atoms, bonds, and unbonded electrons. The atoms (represented by letters) are connected by bonds (pairs of electrons represented by lines), with any “leftover” or unbonded electrons on each atom displayed as dots. For example, here are the Lewis structures of water and ethylene.
With one click of a button, Wolfram|Alpha Pro users can access Step-by-step functionality that will guide them through the process of drawing a Lewis structure.
Wolfram|Alpha now helps users understand the principles behind bonding and chemical structures. With these steps, users can go above and beyond just seeing what the Lewis structure of nitrogen dioxide (NO2) looks like. The Step-by-step interface includes these features:
- It is completely self-contained: All relevant information (valence electron count, electronegativities of atoms, etc.) is inside of the steps if needed.
- Explains why bonds occur and distinguishes between bonding types: The interface determines which bonds should be single, double, or triple and why. This is truly at the heart of chemical bonding. (We give an in-depth explanation of different bonding types below.)
- Points out exceptions: Wolfram|Alpha teaches you how to correctly deal with these “special cases,” so you don’t fear them.
- States interesting properties: Wolfram|Alpha draws your attention when neat things are happening inside of a molecule (special bond types, expanded valence shells, etc). In particular, Wolfram|Alpha will point out when there are multiple ways to draw a molecule rather than keeping you guessing on whether another answer is “as correct” as the given one.
Let’s go through some examples to get a sense of what drawing a Lewis structure entails. In order to do this, we need three basic chemistry facts.
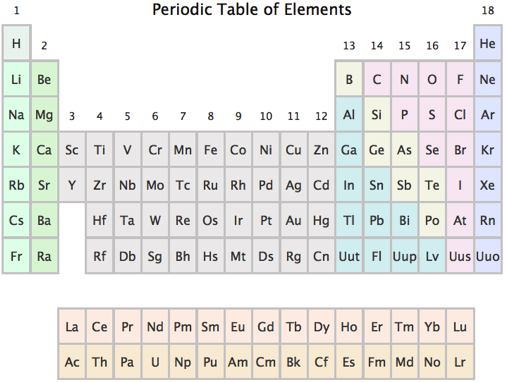
The first fact is a definition: the columns of the periodic table are labeled from 1 to 18, and elements in columns 1, 2, 3, …, 18 are said to be in group 1, 2, 3, …, 18. The group numbers are shown above the columns in the following periodic table.
The second fact is that elements in groups 1, 2, 13, 14, 15, 16, 17, and 18 have 1, 2, 3, 4, 5, 6, 7, and 8 valence electrons, which is the number of electrons they have in their outermost shell (compared to these outermost electrons, the innermost electrons barely have an effect and hence can be ignored). I have skipped over groups 3 through 12 on purpose—more on that below.
The third and final fact we need is that every atom (except hydrogen or helium) wants to have 8 valence electrons. The most common way for atoms to gain additional valence electrons is by sharing electrons and forming covalent bonds. A covalent bond occurs when two atoms each place one of their electrons into the space between them, thereby allowing both atoms to act as if both electrons are a part of their valence shell. By donating one electron into the bond and getting to feel both electrons from the bond, each of the atoms increases its valence electron count by 1 electron. Returning to the Lewis diagram for water:
Oxygen (in group 16) began with 6 valence electrons while both of the hydrogen atoms (group 1) began with 1 valence electron. The oxygen donated 1 electron to bond together with each hydrogen’s electron (note that the two bonds have the colors of both atoms, since each atom donated 1 electron to make up the bond). Thus oxygen now has 8 valence electrons: 4 from its unbonded electron and 4 more from its two covalent bonds (since each bond gives 2 electrons). Both hydrogen atoms feel like they have 2 valence electrons from their bond with oxygen.
The observant reader will note that I have completely skipped over ionic bonding. By convention, Lewis structures only apply to covalently bonded molecules, and we will follow that philosophy here. Other types of bonds (such as hydrogen bonds) are too weak to influence the location of the electrons relative to their atoms, so we are safe in only considering covalent bonds. Additionally, I have completely neglected the transition metals (atoms with group numbers ranging from 3 to 12). Truthfully, the transition metals do not behave with such simple rules as the other elements, so for the purposes of this discussion, we will pretend they do not exist (just close your eyes and pretend!).
Now that we have gotten past the basics, let’s get to some points that you might not hear in any introductory chemistry class. What happens to hydrogen? Is it happy with only one bond? Actually, it is. Hence, oftentimes people have the misconception that all elements in groups 1 and 2 only “want” 2 valence electrons (in chemistry classes, the party line is that having a fully filled s valence shell is more stable than having a partially filled p shell).
Yet that is incorrect: every element in groups 1 and 2 (except hydrogen) wants 8 electrons. Because group 1 elements only have 1 electron, they can only participate in one covalent bond. But any group 2 element (with 2 valence electrons available for bonding) will always have two bonds, and any group 13 element (with 3 valence electrons) will always have at least three bonds (in fact, group 13 elements sometimes manage to snag an extra electron and make four bonds). So the general rule is that all atoms want 8 valence electrons, and even atoms that cannot achieve 8 valence electrons try to get as close as possible. As for the molecules that can covalently bond to get 8 valence electrons, we can (correctly) predict that in general, group 14, 15, 16, and 17 atoms will have four, three, two, and one covalent bonds, respectively. Finally, we expect that group 18 atoms, which start out with 8 valence electrons, will not want to form covalent bonds, and hence will rarely show up in any molecule. It is this property of low reactivity that has led to group 18 elements being referred to as the inert gases or noble gases. (Helium, being a special case, is also considered a noble gas, even though it only has 2 valence electrons.) The following grid shows an example of the typical bonding seen from each group:

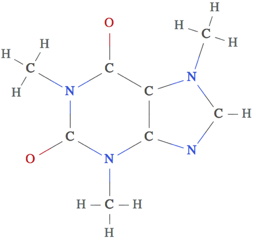
To recap, molecules will covalently bond in order to bump their valence electron count as close to 8 valence electrons as possible. Now that we have this theory under our belt, let’s apply it and figure out the Lewis structure of an important molecule that plays a vital role in many peoples’ lives: caffeine. We begin with the basic layout of caffeine, merely showing which atoms are bonded together but suppressing any double or triple bonds, as well as any unbonded electrons.
Using the group numbers found from the periodic table, hydrogen (group 1), carbon (group 14), nitrogen (group 15), and oxygen (group 16) have 1, 4, 5, and 6 valence electrons, respectively. Remembering that each covalent bond uses up 1 electron from each of the two bonded atoms, we can fill in the remaining electrons on each atom and highlight any atoms that do not have 8 valence electrons (hydrogen is not highlighted because it is the exceptional atom that wants only 2 valence electrons).

We are now faced with a simple puzzle where we want to connect adjacent highlighted atoms with additional bonds until they have 8 valence electrons. There is only one solution:

Having done this warm-up, let’s consider the much larger and significantly more important (not to mention decidedly less unhealthy) molecule ATP. This time, we combine the first two steps together, showing the ATP molecule with single bonds and immediately highlighting all the atoms that want more valence electrons.
The eight highlighted carbon and nitrogen atoms on the bottom-left are very interesting in their own right (in fact, they form aromatic bonds, which are exceedingly interesting!), but we already know how to add bonds to complete their valence shells (hint: it takes four additional bonds). Instead, we will focus on the top-right of ATP where the highlighted oxygen atoms pose a problem. Each of the three highlighted oxygen atoms wants an additional bond in order to have 8 valence electrons, and each oxygen is bonded to a phosphorus atom with an additional electron available to form a bond. But these phosphorus atoms already have 8 valence electrons (in fact, they have 9). So what happens?
At this point, the situation turns into a fight scene. Oxygen wants to form a bond with phosphorus and attain 8 valence electrons while phosphorus wants to stay as close to 8 valence electrons as possible. (You might be wondering why phosphorus cannot happily accept the extra electrons. The answer lies in the fact that the extra electrons phosphorus acquires spill over into its d shell—sticking to my mantra of not discussing transition metals or their like, suffice it to say that phosphorus would prefer 8 valence electrons to 9, and 9 valence electrons to 10). The resolution of this struggle comes from comparing a property called electronegativity, which measures how strongly an atom wants an extra electron (in other words, how strongly an atom is willing to push to gets its way). The atom with the larger electronegativity will win: if oxygen has a larger electronegativity, then it will form a double bond with phosphorus; if phosphorus has the larger electronegativity, then it will remain single bonded to oxygen. As Wolfram|Alpha politely informs us:
Oxygen has the larger electronegativity, and hence we find the complete Lewis structure of ATP.
So, in the end, bonding occurs between two atoms in the following two cases:
1. When two adjacent molecules have an incomplete valence (and hence are both highlighted), they can form an additional bond to bring both atoms closer to 8 valence electrons.
2. A highlighted atom with large electronegativity (oxygen, in the case of ATP) can force an unhighlighted atom with smaller electronegativity (phosphorus in ATP) to expand its valence shell (for technical reasons having to do with the d shell, this can only happen if the unhighlighted atom is on the third row of the periodic table or lower).
So that’s it: bonding in a nutshell. I think we should all give ourselves a big pat on the back and really enjoy this moment.
But don’t get me wrong: this is not the whole story. Among the millions of discovered molecules there are exceptions to practically every rule, ranging from quirky oddities (such as an atom donating both electrons in order to make what is called a dipolar bond) to ridiculous outliers (such as making four covalent bonds, which typically takes 8 electrons, using only 3 electrons). Wolfram|Alpha will gallantly steer through all the stunts even the trickiest molecules can pull and show the correct Lewis structure.
But even some basic molecules can get very tricky. There are a variety of different procedures for generating Lewis structures. One of the most common procedures, which can be found in any standard textbook (such as Principles of Modern Chemistry) or simply by searching “How to draw Lewis structures,” states that after determining which bonds should be made into double or triple bonds, you divvy up the remaining electrons from the most electronegative atom to the least electronegative atom. Unfortunately, this procedure will fail for as small and simple a molecule as nitrogen dioxide NO2; it predicts that of the 11 remaining electrons, 10 should go first and foremost to the more electronegative oxygen atom, leaving the nitrogen atom with a single electron. By contrast, our correct procedure above accounts for the fact that nitrogen started out with 5 electrons, so that after making three bonds it should have 2 unbonded electrons remaining. Similarly, oxygen started with 6 electrons and hence after making either one or two bonds, it should end up with 5 or 4 unbonded electrons, respectively.

Because this common procedure is so pervasive in textbooks and on the internet (as the name suggests), about half of the Lewis structures you get when searching for “NO2 Lewis structure” are wrong. So next time someone shows you the incorrect Lewis structure of NO2, feel free to pull out Wolfram|Alpha and have it lay out the smackdown.
Having come to what appears to be the end of an epic quest to understand Lewis structures, let’s do a quick reality check. The two cases of bonding discussed above are a great starting point, but to be robust enough to handle all the different cases out there, they need to be significantly expanded. For example, consider the class of ions (molecules with extra electrons either added to them or removed from them, giving them a net charge). If we focus on ions with a negative net charge such as phosphate, sulfate, or nitrate, you might suspect that the most electronegative atom (oxygen, in all three cases) will get an additional electron from the net charge. This makes sense, since oxygen naturally has the largest pull on the extra electron. But what happens when all the atoms have the same electronegativity? And what happens when this rule completely breaks down and a less electronegative atom gets the extra electron? The deeper you delve into such cases, the more mysteries seem to pop up. Such trains of thought can spiral out to infinity… and beyond! But that is a good thing: each iteration allows you to better characterize an important class of molecules that can only be competently handled once its scope is completely defined.
At the conclusion of this escapade into bonding, I find it important to step back and discuss the limitations of these results. The most important question to ask is: Do the rules discussed above really mirror the underlying principles governing molecular bonding? If they do, then you would expect to find simple arguments (like F = m a in physics) from which these rules naturally arise. (For example, in ATP, can you calculate the difference in energy between the actual molecule and the analogous version with single bonds between the highlighted oxygen and phosphorus atoms? Could such a calculation be made knowing only the difference in electronegativities of oxygen and phosphorus?) The truth is that no one knows. Chemists are divided about whether you can accurately model what is going on at the atomic level by only considering valence electrons; some chemists believe that you need another theory, such as molecular orbital theory, to truly understand the behavior of electrons. The waters are especially murky here because some chemical principles are derived by trying to explain the trends that we see in the data points currently available. Thus, such statements cannot truly be proved, but they can be disproved with counterexamples. So although the theory above holds up for the substantial chemical database we have at Wolfram|Alpha, I can’t say that some other (potentially crazy and ridiculously complex) molecule out there will come about that will totally shatter this framework.
But when that happens, it is simply time to roll out the ubiquitous exceptions list…
Great post, Tal!
This capability for W|A is very relevant for the classroom.
I have a couple of questions, though, for the chemistry app situation (e.g., ChemDraw or JChem). For your ATP example, why didn’t you mention dative bonds for the P-O bonds? They have often been improperly handled in computational chemistry programs and chemical databases. Most often they are represented by a formal double bond:
P=O
and sometimes as a charge separated pair:
(P^+)-(O^-)
(I’m using the ^ to indicate a superscript) with 6 unbonded electrons around O.
My second question is about the aromatic bonds. The 6-membered ring in the purine can be drawn with two different configurations of alternating single and double bonds. Both are equally correct. I’m sure that Solve (if you are using it behind the scenes) would give both solutions to this problem. Are you considering showing alternative solutions?
My third, and last, question/comment/suggestion is that this capability naturally leads to handling tautomers. Have you thought about taking that step?
Btw, the last time I had to write software to handle bonding and Lewis structures was quite a while ago and was done in FORTRAN. Just imagine how much easier it would have been in Mathematica!
Bob
Thanks for the feedback, Bob. To answer your questions:
1. Indeed, as you pointed out, P=O “double bonds” are a tricky business. Thanks to quantum mechanics, there is contribution from both P=O double bonds as well as P-O single dative bonds.
For example, Linus Pauling calculated (back in the 1960s) that in carbon monoxide, the triple dative bond version (with C and O having formal charges -1 and +1) contributes 50%, the double bond version (with zero formal charges) contributes 40%, and a single bonded version (with C and O having formal charges +1 and -1) contributed 10% (which explains why you will never find the single bonded version in any textbooks!).
Determining which type of bond contributes the most depends upon the molecule, and it is a difficult task both experimentally and theoretically. F or the time being, we are taking the overly-simplistic approach of describing P=O “double bonds” as formal double bonds, but we will gladly update our database as new experiments come to light.
2. Currently we comment upon resonance structures – including the purine ring – within the text of the steps (more precisely, within the last step). Based on user feedback, we may decide to draw all such resonance structures explicitly in the future. (By the way, behind the scenes our Graph functionality plays a central role in such cases.)
3. Tautomers, and more generally structural isomers, are an excellent idea that we are currently looking into. Thanks!
Now that you have Lewis structures have you considered moving to electronic and molecular geometries?
Another great step by step chemistry topic would be point group analysis.
Thanks for the excellent work.
Both of those suggestions will be great additions to our 3D structure diagrams. I will definitely add them to our future projects.
Will there be support for explanation of mechanisms? If so, that would be fantastic!
Dear Tal,
Your writing style is great. Tell me that you have written a chemistry book !?
This is the greatest compliment I have ever received!
I will not be easy until W|A can explain how proteins are folded. That said, this is a welcome addition! Thank you for all the hard work.
Hello! Ths is a great job,although I didn’t understand how then does N2O4 form?



 Comments Off
Comments Off