Explore Mathematical Games with Wolfram|Alpha

Game theory is a rich branch of mathematics that deals with the analysis of games, where, mathematically speaking, a “game” can be defined as a conflict involving gains and losses between two or more opponents who follow formal rules.

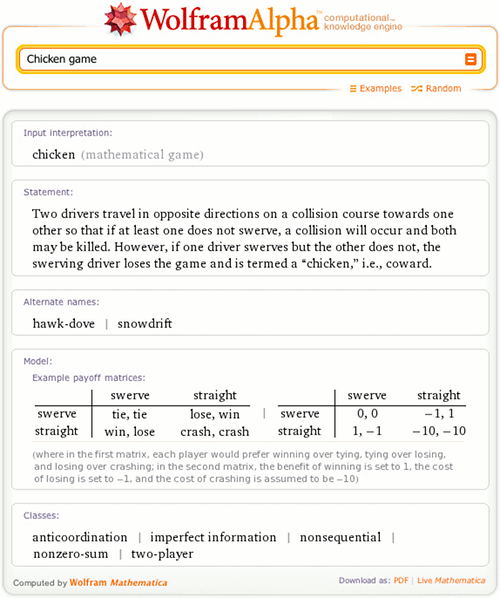
Mathematical games can be very simple, such as the game of chicken (which is not recommended in practice):

(The chicken game is featured, among other places, in movies such as Rebel without a Cause and Highlander). “Colonel Blotto” is a more complicated resource-allocation problem:

The latest release of Wolfram|Alpha now knows about a variety of famous mathematical games and can return many computational details and mathematical properties about them.

As illustrated in the screen capture above, mathematical games may be categorized into a number of different classes. For example, the classic tic-tac-toe game is a two-player game that is fair (not biased toward either player), futile (permits a draw when played properly by both players), and sequential (moves alternate between players).

More precise characterizations of a game include the payoff matrix (an m x n matrix that gives the possible outcome of a two-person zero-sum game when player A has m possible moves and player B has n moves) and the decision tree (a tree-like graph of decisions and their potential outcomes), both of which are illustrated above. Both these tools can be used to analyze games in an attempt to determine optimal strategies for players, which is one of the primary aims of game theory.

Support for more games and more game-theoretic properties (e.g., Nash equilibrium) is under way. But in the meantime, Wolfram|Alpha already does more than just answer the question “Shall we play a game?” by providing you with some useful information about a number of the games you might actually want to play.