Find Figurate Numbers in Wolfram|Alpha

Want to know if you and your 20 teammates can march in perfect triangular formation in a parade? Or maybe you want to know how many glasses you’ll need in order to break the world record for largest champagne pyramid (currently 60 stories high, with 37,820 glasses).

Whether you’re stacking watermelons or water-skiers or just playing with dots on paper, if you want to make a perfect geometrical formation, then you’re interested in “figurate” numbers. These are numbers for which that number of things can be arranged into a perfect geometrical shape, such as a triangle (in the case of the “triangular numbers”) or a triangular pyramid (AKA, a tetrahedron), which is the shape of champagne pyramids.

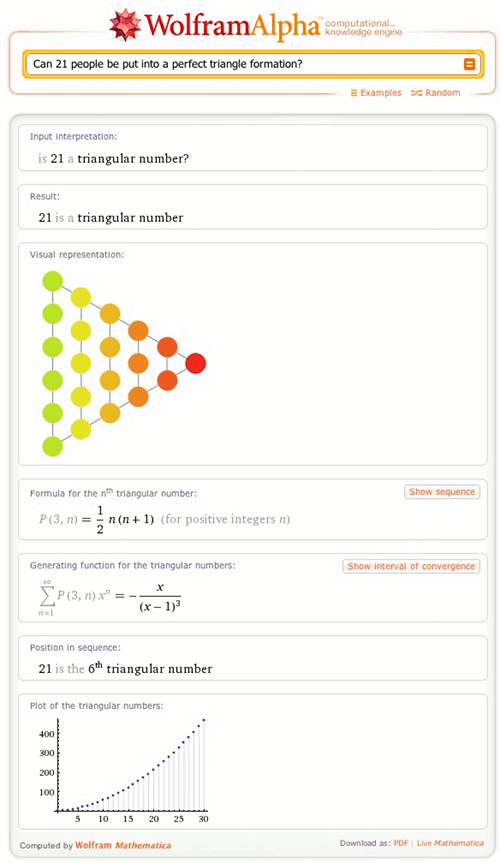
Wolfram|Alpha now has the ability to tell you if a given number is any figurate number. Entering our first question, “Can 21 people be put into a perfect triangle formation?”, into Wolfram|Alpha gives an affirmative, along with a diagram and other useful information:

To check out the current world-record champagne pyramid, simply enter:

The fact that 37,820 is the 60th tetrahedral number tells us that the record champagne pyramid is indeed 60 stories high (a single glass counts as the first, or smallest, tetrahedron). To see how to break the record, we could click the “Show sequence” button, which will show us all the tetrahedral numbers we want, including the one just after 37,820.

So the next tetrahedral number is 39,711—that’s only 1,892 more glasses!

In addition to all the standard kinds of figurate numbers, such as triangular numbers and square numbers, Wolfram|Alpha knows about some more obscure types:

Notice that when the answer is negative, Wolfram|Alpha tells you the nearest numbers of that type. In this case, 33 and 185 are the closest Ha?y rhombic dodecahedral numbers.

Figurate numbers generalize in many ways. “Polygonal numbers” generalize the triangular, square, and pentagonal numbers by adding more sides to the formation. Wolfram|Alpha can tell you if a number is polygonal for any number of sides:

There are also the “centered” polygonal numbers, which are arrangements of polygons centered around a single thing. Wolfram|Alpha can tell you if a number is centered polygonal for any number of sides:

Triangles also generalize into more dimensions, called “simplices” or “polytopes”. For example, the three-dimensional simplex is just our old friend the tetrahedron, or three-sided pyramid. This is also the formation in which cannonballs are typically stacked. Wolfram|Alpha knows about every simplicial polytope number in every dimension:

Now you can use Wolfram|Alpha to help you construct most kinds of regular formations. Whether you’re an artist or a mathematician, or just having fun, we hope you enjoy this new feature!