Non-periodic Substitution Tilings

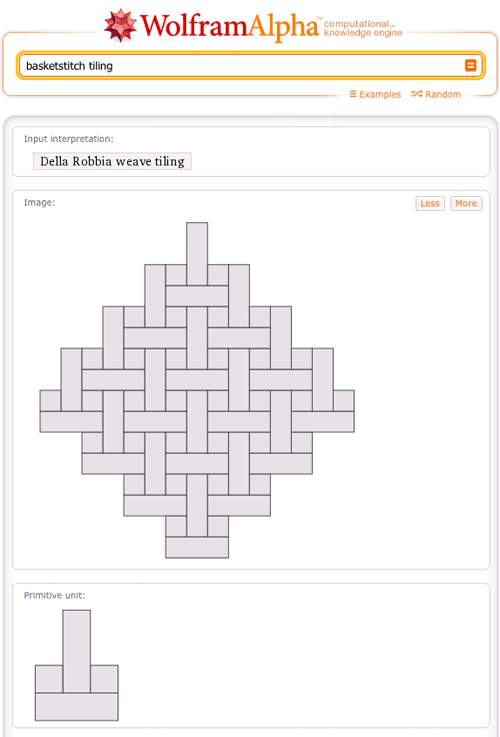
Periodic tilings (also known as tessellations) are often beautiful arrangements of one or more shapes, known as tiles, into regular patterns, which if extended infinitely are capable of covering the entire plane without gaps. Wolfram|Alpha has possessed detailed knowledge on more than 50 common (and uncommon) varieties of periodic tilings for some time, as illustrated, for example, in the case of the basketstitch tiling:

Periodic tilings possess an individual motif (more formally known as a primitive unit) that is repeated iteratively in a predictable (periodic) way. Such tilings are therefore intimately related to the set of symmetry groups of the plane, known as wallpaper groups. While the most general set of geometric similarity (i.e., shape-preserving) operations in the plane includes rotation (change in angle), dilation/expansion (change in size), reflection (flipping about an axis), and translation (change in position), only translation is needed to produce a periodic tiling from a correctly constructed primitive unit.

Periodic tilings have been the subject of much mathematical and artistic study throughout mankind’s recorded history, but important developments in the more challenging case of tilings that are not periodic have come mostly in the last half-century. While periodic tilings can be defined as tilings possessing a primitive unit and an associated translation vector, tilings that are not periodic may be either non-periodic (lacking a translation vector on a primitive unit) or aperiodic (in addition to being non-periodic, no periodic tiling is possible for any arrangement of the given tile set).

The existence of non-periodic tilings can be demonstrated by means of the simple case of domino tiling:

Begin by considering the periodic case. The tiling above uses substitution rules that subdivide each domino into four 1/4-size dominoes:

Now, instead of building a domino tiling by subdividing individual dominoes or by tiling a square and then repeating that arrangement on a grid, consider placing dominoes randomly next to one other. Random arrangements are not periodic, and thus a non-periodic tiling, but not an aperiodic one, since we have already established that periodic tilings exist for dominoes.

An obvious question to ask is whether aperiodic tilings exist. In 1619, Kepler came close to constructing such a tiling using regular pentagons, pentagrams, decagons, and “fused decagon pairs” in the arrangement now known as Kepler’s monsters:

It turns out that the shapes in Kepler’s monsters can be arranged into a large diamond that serves as a primitive unit, so in fact they can tile the plane periodically. However, they became the basis of an aperiodic tiling when Roger Penrose studied them and subsequently devised a set of tiles that never produces a primitive unit. The reduced set of tiles he ultimately constructed are now known as kites and darts, and the aperiodic tiling they produce (aperiodic, since rules or edge modifications can be added to prevent a kite and dart from making a diamond or other periodic motif) is commonly known as a Penrose tiling:

This tiling is just one member of a new class of tilings that are now available in Wolfram|Alpha in computable form. To describe this class more completely, note that in addition to producing aperiodic tilings, Penrose tiles are also an example of what’s known as a substitution tiling, since the kite and dart can be replaced via the following substitution to produce a tiling:

The full set of substitution tilings that have recently been added to Wolfram|Alpha is illustrated below:

Some such tilings of particular note include the L-tetromino tiling, tromino tiling, and Ammann chair tiling:

The Amman chair is of interest because it uses a single tile whose dimensions are intimately linked with the golden ratio ?, as shown in the following diagram:

Please feel free to explore substitution tilings with the aid of Wolfram|Alpha. As is not uncommon in mathematics, it is both amazing and rewarding to observe what beautiful structures and results arise from so simple a problem as tiling of the plane. And while most people will probably restrict their consideration of such tilings to online exploration, the more mathematically minded among you may perhaps wish to consider them in more detail the next time you’re retiling your kitchen or bathroom floor 🙂

This post was written by Ed Pegg Jr. and Eric Weisstein.