Need a tutor for solving equations? Solving equations is just one of hundreds of mathematical tasks that can be done using Wolfram|Alpha. Wolfram|Alpha can solve equations from middle school level all the way through college level and beyond. So next time you are stumped on an equation, consult Wolfram|Alpha for a little help.
Let’s start with the simpler stuff. Wolfram|Alpha can easily solve linear and quadratic equations, and even allows you to view a step-by-step solution of each problem.
What if the roots of the equation are complex? No worries; Wolfram|Alpha has no trouble solving equations over the complex plane.
Wolfram|Alpha can also solve cubic and quartic equations in terms of radicals.
Of course, some solutions are too large or cannot be represented in terms of radicals; Wolfram|Alpha will then return numerical solutions with a “More digits” button.
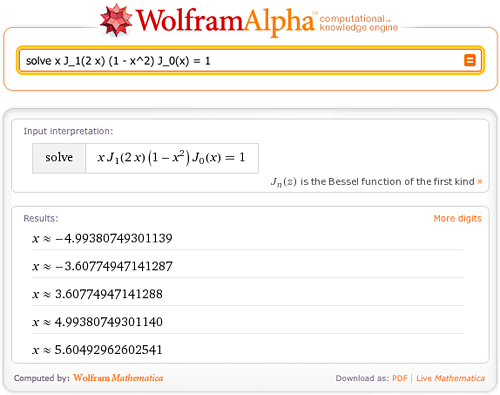
Conveniently, Wolfram|Alpha not only solves polynomial equations but also equations involving trigonometric, hyperbolic, or even special functions, as in the following example.
Do you want to solve an equation over the reals? Just tell Wolfram|Alpha to restrict the domain.
Wolfram|Alpha can also solve systems of linear and nonlinear equations.
In the near future, it will be possible to see step-by-step solutions for systems of linear equations
Let’s take it one step further. Do you need to solve a system of polynomial congruences? Wolfram|Alpha is not stumped!
Are you working with recurrence relations? Wolfram|Alpha can solve recurrence equations in seconds.
For more, check out the Examples pages. The underlying technology used here are the Mathematica functions FindInstance, Solve, RSolve, FindRoot, NSolve and Reduce.
Remember that these are just a few of the ways that Wolfram|Alpha can solve equations—try some of your own math problems and explore other equation types. In a future blog post, we’ll show you how Wolfram|Alpha can also solve inequalities and systems of inequalities.
I noticed that it can show steps. I was thrilled when I typed in 1/(1-x^2) as it not only split it into partial fractions, but it revealed in the relationship that the above has with tanh^-1(x) upon integration.
This makes it an even better reference and educational resource, but I was wondering if there was any software available for Mathematica to enable similar functionality.
The solutions to fourth degree polynomial equations can always be expressed in terms of radicals. The solutions to the quartic in the given example all were less than 6 in absolute value. “Of course, some solutions are too large or cannot be represented in terms of radicals”?!
Perhaps Wolfram|Alpha does not want to display the exact solutions because they are messy, but those solutions can be expressed in terms of radicals and are not large.
It is sad that wolfram doesn’t have a Polish translation.
Unfortunately, someone bought the pl domain.
I used wolfram alpha to teach my student about solving equations,I put some examples in my blog, htttp://abdulkarim.wordpress.com
Still has a long way to go. I wanted to solve (1 + 1.6*10^-19*x/(1.38*10^-23 * 300))*exp(1.6*10^-19*x/(1.38*10^-23 * 300)) = 35.68/30*10^-9 and it returned x = 0.025875 W_n((3568000000 e)/3)-0.025875 and n element Z, as the result. Strange. I did same thing with Matlab fsolve and got 0.464 which is the solution I was looking for. Alpha still has a long way to go. I didn’t think I would still need MATLAB for little things like this…..
I cannot get Wolfram|alpha to solve a system (linear or otherwise) larger than 3 by 3. Has anyone been able to do this? Yes, I have read all of the tutorials and I am familiar with the RREF command, but I’d just like to enter in the equations and see the solution. Imagine telling someone to get the solution to a 5 by 5 system, but having to teach them basic matrix operations first. That’s kind of annoying.
All the previous notwithstanding, I very much like Wolfram|alpha and will continue to use it in the future. I just wish solving a “larger” system was easily done.